What Do You Learn in Algebra 1 Honors? This course is a challenging and rewarding exploration of foundational algebraic concepts, taking you beyond the basics and into a deeper understanding of mathematical relationships. You’ll delve into the world of variables, expressions, equations, and inequalities, learning how to manipulate them to solve real-world problems.
From mastering the fundamentals of solving linear equations to grappling with the complexities of quadratic equations and functions, you’ll develop a comprehensive understanding of algebraic principles. You’ll learn how to analyze and interpret data, applying statistical methods to make informed decisions.
You’ll even explore the fascinating world of probability, learning how to quantify the likelihood of events and make predictions about the future.
Foundations of Algebra
Algebra 1 Honors builds upon your existing math knowledge and introduces you to the fundamental concepts of algebra, which are essential for understanding more advanced math concepts. This foundation will enable you to solve complex problems in various fields like science, engineering, and finance.
Variables
Variables are symbols, usually letters, that represent unknown quantities. They allow us to express relationships between numbers and quantities in a concise and general way.For example, if you want to represent the cost of buying “x” apples at $1.50 each, you can use the variable “x” to represent the number of apples.
The total cost can then be expressed as 1.50x.
Expressions
Expressions are combinations of variables, constants, and mathematical operations (like addition, subtraction, multiplication, and division). They represent a mathematical value that can be evaluated by substituting specific values for the variables.For example, 2x + 3 is an expression. If x = 5, then the expression evaluates to 2(5) + 3 = 13.
Equations
Equations are mathematical statements that express the equality between two expressions. They contain an equal sign (=) and aim to find the values of variables that make the equation true.For example, 2x + 3 = 11 is an equation. Solving for x, we find that x = 4.
Order of Operations
The order of operations is a set of rules that dictate the sequence in which operations should be performed in an expression. It ensures that expressions are evaluated consistently, regardless of who is evaluating them. The order of operations is often remembered using the acronym PEMDAS:
Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)
For example, in the expression 2 + 3
- 4, we perform the multiplication first (3
- 4 = 12) and then the addition (2 + 12 = 14).
2. Linear Equations and Inequalities
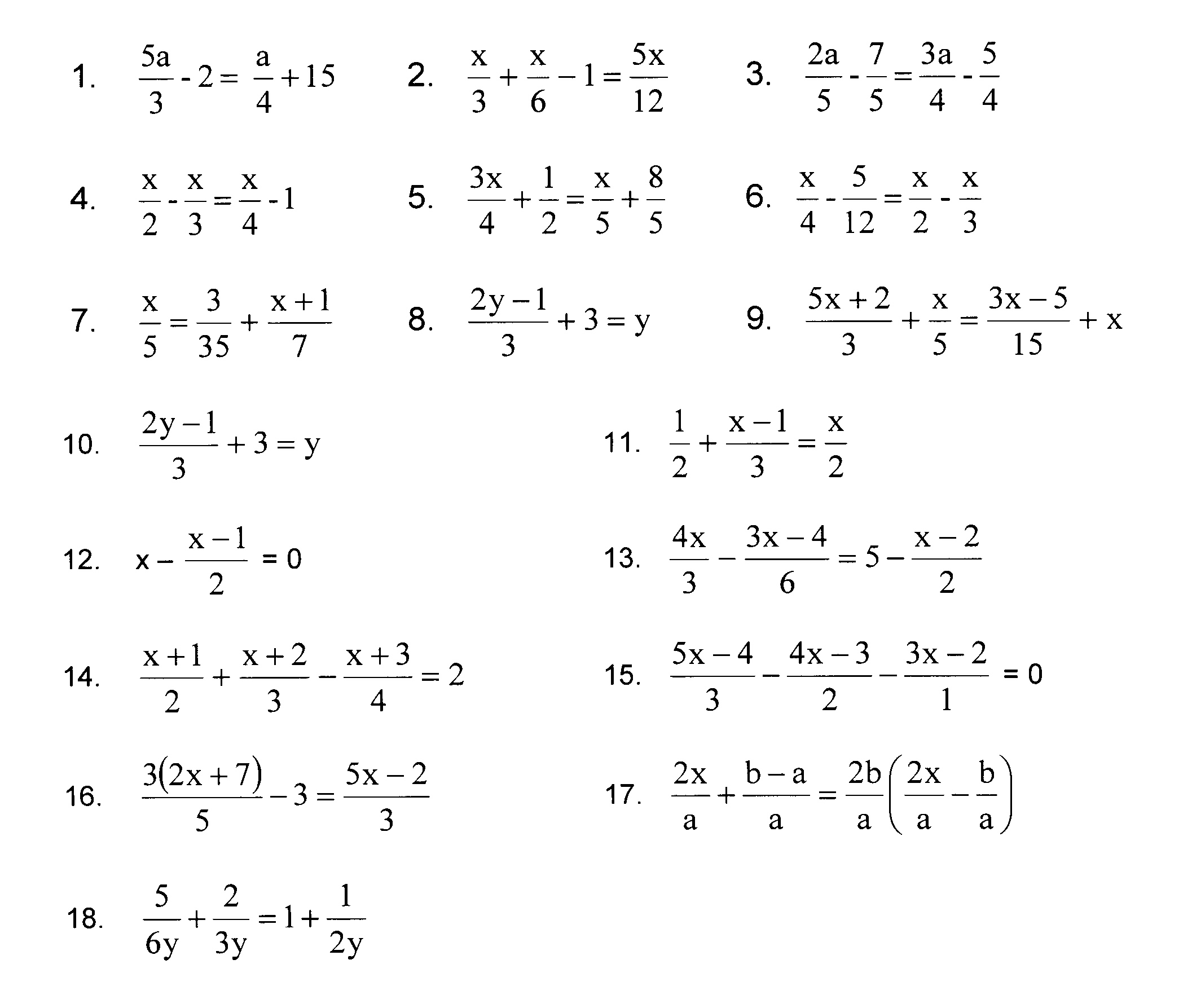
Linear equations and inequalities are fundamental concepts in algebra, providing the foundation for understanding more complex mathematical ideas. They are used extensively in various fields, including finance, science, and engineering, to model and solve real-world problems. In this section, we will delve into the methods for solving linear equations and inequalities, explore their properties, and understand their applications.
2.1 Solving Linear Equations
Solving linear equations involves finding the value(s) of the unknown variable that make the equation true. There are two primary methods for solving systems of linear equations: substitution and elimination.
2.1.1 Substitution Method
The substitution method is a technique for solving systems of linear equations by solving one equation for one variable and substituting that expression into the other equation. This process eliminates one variable, allowing you to solve for the remaining variable.
Once you find the value of one variable, you can substitute it back into either of the original equations to solve for the other variable.Here is an example to illustrate the substitution method: Example:Solve the following system of equations using the substitution method:“`
x + y = 7
x
- 2y =
- 1
“` Step 1:Solve one equation for one variable. Let’s solve the second equation for
-x*
“`x
- 2y =
- 1
x = 2y
1
“` Step 2:Substitute the expression for
-x* into the first equation
“`
- (2y
- 1) + y = 7
“` Step 3:Simplify and solve for
-y*
“`
- y
- 2 + y = 7
- y = 9
y = 9/5“` Step 4:Substitute the value ofy* back into either of the original equations to solve for
-x*. Let’s use the second equation
“`x
- 2(9/5) =
- 1
x =
1 + 18/5
x = 13/5“`Therefore, the solution to the system of equations is
- x = 13/5* and
- y = 9/5*.
2.1.2 Elimination Method
The elimination method is another technique for solving systems of linear equations. It involves manipulating the equations to eliminate one of the variables by adding or subtracting the equations together. This process results in a single equation with one variable, which can then be solved.
Once you find the value of one variable, you can substitute it back into either of the original equations to solve for the other variable.Here is a table illustrating the steps involved in the elimination method:| Step | Description | Goal ||—|—|—|| 1 | Multiply one or both equations by a constant to make the coefficients of one variable opposites.
| To create opposite coefficients for one variable. || 2 | Add or subtract the equations together to eliminate one variable. | To eliminate one variable from the system. || 3 | Solve the resulting equation for the remaining variable.
| To find the value of the remaining variable. || 4 | Substitute the value of the solved variable back into either of the original equations. | To solve for the other variable. |
2.1.3 Comparison of Methods
The substitution and elimination methods are both effective for solving systems of linear equations. The choice of method depends on the specific problem and personal preference.The substitution method is generally preferred when one of the equations is already solved for one variable or when it is easy to solve for one variable.
It can be less efficient when dealing with equations with complex coefficients.The elimination method is often more efficient when the coefficients of one variable are already opposites or when it is easy to manipulate the equations to make them opposites.
It can be less intuitive than the substitution method for some students.
2.2 Properties of Equality and Inequality
The properties of equality and inequality are fundamental principles that govern how equations and inequalities are manipulated. These properties ensure that the solutions obtained are valid and consistent with the original expressions.Here is a table summarizing the key properties of equality and inequality:| Property | Mathematical Representation | Description ||—|—|—|| Reflexive Property of Equality|a = a* | Any quantity is equal to itself.
|| Symmetric Property of Equality|If a = b, then b = a* | If one quantity is equal to another, then the second quantity is equal to the first. || Transitive Property of Equality|If a = b and b = c, then a = c* | If one quantity is equal to a second quantity, and the second quantity is equal to a third quantity, then the first quantity is equal to the third quantity.
|| Addition Property of Equality|If a = b, then a + c = b + c* | Adding the same quantity to both sides of an equation does not change the equality. || Subtraction Property of Equality|
- If a = b, then a
- c = b
- c* | Subtracting the same quantity from both sides of an equation does not change the equality. |
| Multiplication Property of Equality|If a = b, then ac = bc* | Multiplying both sides of an equation by the same non-zero quantity does not change the equality. || Division Property of Equality|If a = b and c ≠ 0, then a/c = b/c* | Dividing both sides of an equation by the same non-zero quantity does not change the equality.
|| Reflexive Property of Inequality|-a < a* or -a > a* | A quantity is not less than or greater than itself. || Transitive Property of Inequality|-If a < b and b < c, then a < c* | If one quantity is less than a second quantity, and the second quantity is less than a third quantity, then the first quantity is less than the third quantity. | | Addition Property of Inequality|-If a < b, then a + c < b + c* | Adding the same quantity to both sides of an inequality does not change the direction of the inequality. | | Subtraction Property of Inequality|-If a < b, then a - c < b - c* | Subtracting the same quantity from both sides of an inequality does not change the direction of the inequality. | | Multiplication Property of Inequality|-If a < b and c > 0, then ac < bc* | Multiplying both sides of an inequality by the same positive quantity does not change the direction of the inequality. | | Division Property of Inequality|-If a < b and c > 0, then a/c < b/c* | Dividing both sides of an inequality by the same positive quantity does not change the direction of the inequality. | | Multiplication Property of Inequality |If a < b and c < 0, then ac > bc* | Multiplying both sides of an inequality by the same negative quantity reverses the direction of the inequality. || Division Property of Inequality|If a < b and c < 0, then a/c >b/c* | Dividing both sides of an inequality by the same negative quantity reverses the direction of the inequality. |
2.3 Solving Linear Inequalities
Solving linear inequalities involves finding the range of values for the unknown variable that make the inequality true. The process of solving linear inequalities is similar to solving linear equations, but with a few key differences.
2.3.1 Step-by-Step Guide
Here is a step-by-step guide for solving linear inequalities:* Step 1:Simplify both sides of the inequality by combining like terms.
Step 2
Use the properties of inequality to isolate the variable on one side of the inequality. This involves adding, subtracting, multiplying, or dividing both sides by the same quantity, keeping in mind that multiplying or dividing by a negative number reverses the direction of the inequality.
Step 3
Express the solution in interval notation or set-builder notation.
2.3.2 Graphing Solutions
The solution to a linear inequality can be represented graphically on a number line. The solution set is the range of values that satisfy the inequality. Example:Solve the following linear inequality and graph the solution on a number line:“`2x + 3 < 7 ```Step 1:Subtract 3 from both sides of the inequality:“`2x < 4 ```Step 2:Divide both sides by 2:“`x < 2 ```Step 3:Graph the solution on a number line.
The solution is all values ofx* that are less than 2. This is represented by an open circle at 2 and a line extending to the left.[Insert image of a number line with an open circle at 2 and a line extending to the left]
2.3.3 Difference Between Equations and Inequalities
The solution to a linear equation is a specific value or set of values that make the equation true. In contrast, the solution to a linear inequality is a range of values that make the inequality true. Example:* The solution to the equation
- 2x + 3 = 7* is
- x = 2*. This means that only the value
- x = 2* satisfies the equation.
- The solution to the inequality
-2x + 3 < 7* is -x < 2*. This means that any value of -x* less than 2 satisfies the inequality.
3. Systems of Linear Equations
A system of linear equations is a set of two or more linear equations that share the same variables. These equations represent lines, and the solution to the system is the point where the lines intersect.
Understanding Systems of Linear Equations
A system of linear equations can have different types of solutions depending on the relationship between the lines. * Consistent System:A system where the lines intersect at one point. This point represents the unique solution to the system.
Inconsistent System
A system where the lines are parallel and never intersect. This means there is no solution to the system.
Dependent System
A system where the lines are coincident, meaning they are the same line. This indicates that there are infinitely many solutions, as every point on the line is a solution.The solutions to a system of linear equations can be represented graphically as the point of intersection of the lines.
Methods for Solving Systems of Linear Equations
There are several methods for solving systems of linear equations:
Graphing
Graphing involves plotting the lines represented by each equation and identifying the point of intersection. This point represents the solution to the system.* Step 1:Solve each equation for y to get the slope-intercept form (y = mx + b).
Step 2
Plot the y-intercept (b) of each line.
Step 3
Use the slope (m) to find additional points on each line.
Step 4
Draw a line through the points for each equation.
Step 5
Identify the point where the lines intersect. This point is the solution to the system. Example:Solve the system of equations:
- y = 2x + 1
- y =
- x + 4
Solution:
- The equations are already in slope-intercept form.
- The y-intercept of the first equation is 1, and the y-intercept of the second equation is 4.
- The slope of the first equation is 2, so from the y-intercept (1, 0), move up 2 units and right 1 unit to find another point (2, 3).
- The slope of the second equation is
- 1, so from the y-intercept (0, 4), move down 1 unit and right 1 unit to find another point (1, 3).
- Draw a line through the points for each equation. The lines intersect at the point (1, 3).
Therefore, the solution to the system is x = 1 and y = 3.
Substitution
The substitution method involves solving one equation for one variable and substituting that expression into the other equation. This eliminates one variable, allowing you to solve for the remaining variable.* Step 1:Solve one of the equations for one variable in terms of the other variable.
Step 2
Substitute the expression from Step 1 into the other equation.
Step 3
Solve the resulting equation for the remaining variable.
Step 4
Substitute the value found in Step 3 back into either of the original equations to solve for the other variable. Example:Solve the system of equations:
- 2x + y = 5
- x
- y = 1
Solution:
1. Solve the second equation for x
x = y + 1
2. Substitute the expression for x into the first equation
2(y + 1) + y = 5
3. Simplify and solve for y
2y + 2 + y = 5; 3y = 3; y = 1
4. Substitute y = 1 into either of the original equations to solve for x. Let’s use the second equation
x
1 = 1; x = 2
Therefore, the solution to the system is x = 2 and y = 1.
Elimination
The elimination method involves manipulating the equations to eliminate one variable by adding or subtracting the equations together.* Step 1:Multiply one or both equations by a constant so that the coefficients of one variable are opposites.
Step 2
Add or subtract the equations to eliminate one variable.
Step 3
Solve the resulting equation for the remaining variable.
Step 4
Substitute the value found in Step 3 back into either of the original equations to solve for the other variable. Example:Solve the system of equations:
- 3x + 2y = 7
- x
- 2y = 1
Solution:The coefficients of y are already opposites.
2. Add the equations together to eliminate y
4x = 8
3. Solve for x
x = 2
4. Substitute x = 2 into either of the original equations to solve for y. Let’s use the second equation
2
- 2y = 1;
- 2y =
- 1; y = 1/2
Therefore, the solution to the system is x = 2 and y = 1/2.
Comparing Methods
| Method | Advantages | Disadvantages ||—|—|—|| Graphing | Visual representation of the solution, easy to understand | Can be inaccurate if the lines are not drawn precisely, may not be suitable for systems with fractional or irrational solutions || Substitution | Relatively simple and straightforward | May involve complex algebraic manipulations || Elimination | Efficient for solving systems with multiple equations, can handle fractional or irrational solutions | Requires careful manipulation of equations |
Real-World Applications
Systems of linear equations can be used to solve a variety of real-world problems. Here are a few examples:* Mixing Solutions:A chemist needs to mix two solutions, one containing 10% acid and the other containing 30% acid, to create 100 ml of a solution containing 25% acid.
How much of each solution should the chemist use?
Let x represent the amount of the 10% solution and y represent the amount of the 30% solution.
The total amount of solution is x + y = 100 ml.
- The total amount of acid is 0.10x + 0.30y = 0.25
- 100 = 25 ml.
Solving this system of equations will give us the amount of each solution needed.* Distance, Rate, and Time:Two cars leave the same location at the same time, traveling in opposite directions. One car travels at 60 mph, and the other travels at 70 mph.
How long will it take for the cars to be 260 miles apart?
Let t represent the time in hours.
The distance traveled by the first car is 60t.
The distance traveled by the second car is 70t.
The total distance between the cars is 60t + 70t = 260 miles.
Solving this system of equations will give us the time it takes for the cars to be 260 miles apart.* Supply and Demand:The supply and demand equations for a particular product are given by:
Supply
p = 2q + 10
Demand
p =
3q + 50
where p is the price per unit and q is the quantity demanded. What is the equilibrium price and quantity for this product?
Equilibrium occurs when supply equals demand, so we need to solve the system of equations.
Solving this system of equations will give us the equilibrium price and quantity.
Writing
Scenario:You and your friend are planning a trip to the amusement park. You want to ride the roller coaster, but your friend is afraid of heights and only wants to ride the Ferris wheel. You agree to ride the roller coaster first and then meet your friend at the Ferris wheel.
The roller coaster has a 20-minute wait time, and the Ferris wheel has a 15-minute wait time. You want to be at the Ferris wheel at 2:00 pm. Problem:What time should you start riding the roller coaster to make it to the Ferris wheel at 2:00 pm?
Solution:Let x be the time you start riding the roller coaster and y be the time you arrive at the Ferris wheel.* Equation 1: y = x + 20 (You arrive at the Ferris wheel 20 minutes after you start the roller coaster)
Equation 2
y = 2:00 pm
15 minutes = 1
45 pm (You need to arrive at the Ferris wheel at 1:45 pm to have 15 minutes to ride)Now, we have a system of equations:* y = x + 20
y = 1
45 pmSubstitute the second equation into the first equation:* 1:45 pm = x + 20Solving for x:* x = 1:45 pm
20 minutes = 1
25 pmTherefore, you should start riding the roller coaster at 1:25 pm to arrive at the Ferris wheel at 2:00 pm.
4. Functions and Their Graphs
Functions are a fundamental concept in algebra, representing a relationship between inputs and outputs. They are essential for understanding various mathematical concepts and applications. In this section, we will explore the definition of functions, their types, and key features of their graphs.
We will also delve into the process of graphing linear functions and their inverses.
Defining Functions and Their Types
A function is a rule that assigns each input value to exactly one output value. This relationship can be represented in various ways, including equations, tables, and graphs.
- Linear Functions: Linear functions are characterized by a constant rate of change, meaning that the output changes by a fixed amount for each unit change in the input. The standard form of a linear function is y = mx + b, where m represents the slope (rate of change) and b represents the y-intercept (the point where the graph crosses the y-axis).
For example, the function y = 2x + 1 is a linear function with a slope of 2 and a y-intercept of 1.
- Quadratic Functions: Quadratic functions are characterized by a U-shaped graph called a parabola. The standard form of a quadratic function is y = ax² + bx + c, where a, b, and c are constants. The coefficient ‘a’ determines the direction of the parabola (upwards if a > 0, downwards if a < 0), and the vertex of the parabola represents the maximum or minimum point of the function. For example, the function y = x² - 4x + 3 is a quadratic function with a vertex at (2, -1).
- Exponential Functions: Exponential functions exhibit a rapid increase or decrease in their output values as the input changes. The standard form of an exponential function is y = ab^x, where ‘a’ represents the initial value (the y-intercept) and ‘b’ represents the growth or decay factor.
If b > 1, the function represents exponential growth, and if 0 < b < 1, it represents exponential decay. For example, the function y = 2^x is an exponential function with an initial value of 1 and a growth factor of 2.
Key Features of Function Graphs
Understanding the key features of function graphs allows us to analyze and interpret their behavior. These features include:
- Slope: The slope of a line is a measure of its steepness and direction. It is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. For example, if the slope of a line is 2, it means that for every 1 unit increase in the x-value, the y-value increases by 2 units.
- Intercepts: The x-intercept is the point where the graph of a function crosses the x-axis, and the y-intercept is the point where it crosses the y-axis. To find the x-intercept, set y = 0 in the function’s equation and solve for x.
To find the y-intercept, set x = 0 and solve for y.
- Domain and Range: The domain of a function is the set of all possible input values, and the range is the set of all possible output values. The domain and range can be determined by examining the graph of the function or by analyzing its equation.
For example, the domain of the function y = 2x + 1 is all real numbers, and the range is also all real numbers.
Graphing Linear Functions and Their Inverses
Graphing linear functions is a straightforward process using their slope-intercept form (y = mx + b).
- Graphing Linear Functions: To graph a linear function, start by plotting the y-intercept (b). Then, use the slope (m) to find another point on the line. For example, if the slope is 2, move 1 unit to the right and 2 units up from the y-intercept to find another point.
Connect the two points to draw the line.
- Inverse Functions: The inverse of a function reverses the input and output values. If a function takes an input x and produces an output y, its inverse takes the output y and produces the input x. For a linear function, finding the inverse involves switching the x and y variables and solving for y.
For example, the inverse of the function y = 2x + 1 is x = 2y + 1, which can be rewritten as y = (x – 1)/2.
- Graphing Inverse Functions: The graph of the inverse function is a reflection of the original function’s graph across the line y = x. To graph the inverse, you can plot points from the original function’s graph and then switch their x and y coordinates to obtain points on the inverse function’s graph.
Polynomials and Factoring
Polynomials are expressions that involve variables and constants, combined using addition, subtraction, and multiplication. They are a fundamental concept in algebra and play a crucial role in solving equations, understanding graphs, and modeling real-world situations. Factoring polynomials is the process of breaking down a polynomial into simpler expressions, often by finding their factors.
This process can help us solve equations, simplify expressions, and gain deeper insights into the behavior of polynomials.
Types of Polynomials
Polynomials can be classified based on the number of terms they have. Here are some common types:
- Monomial: A monomial is a polynomial with only one term. For example, 3x, 5y 2, and 2 are monomials.
- Binomial: A binomial is a polynomial with two terms. For example, x + 2, 2y – 5, and 3a 2+ 4b are binomials.
- Trinomial: A trinomial is a polynomial with three terms. For example, x 2+ 2x + 1, 2y 2– 3y + 1, and 4a 2+ 5ab + b 2are trinomials.
Factoring Polynomials
Factoring polynomials involves finding expressions that, when multiplied together, result in the original polynomial. Here are some common factoring techniques:
Greatest Common Factor (GCF)
The greatest common factor (GCF) of a polynomial is the largest expression that divides into each term of the polynomial. To factor out the GCF, we simply divide each term by the GCF and write the result in parentheses. For example, to factor 6x 2+ 12x, we first find the GCF of 6x 2and 12x, which is 6x.
Then, we divide each term by 6x and get:
6x2+ 12x = 6x(x + 2)
Difference of Squares
The difference of squares pattern states that the difference of two perfect squares can be factored as the product of the sum and difference of their square roots. This can be represented as:
a2
- b 2= (a + b)(a
- b)
For example, to factor x 2
- 9, we recognize that both x 2and 9 are perfect squares (x 2= x
- x and 9 = 3
3). Applying the difference of squares pattern, we get
x2
- 9 = (x + 3)(x
- 3)
Trinomial Factoring
Factoring trinomials involves finding two binomials that multiply to give the original trinomial. This process often involves trial and error, but there are some helpful strategies:
- Identify the coefficients: Identify the coefficients of the trinomial. For example, in the trinomial x 2+ 5x + 6, the coefficients are 1, 5, and 6.
- Find two numbers: Find two numbers that multiply to give the constant term (6 in this case) and add up to the coefficient of the middle term (5 in this case). In this example, the numbers 2 and 3 satisfy these conditions (2
3 = 6 and 2 + 3 = 5).
- Write the factors: Use the two numbers found in step 2 to write the factored form of the trinomial. In this case, the factored form is (x + 2)(x + 3).
Solving Equations Using Factoring
Factoring polynomials can be used to solve equations by setting the polynomial equal to zero and finding the values of the variable that make the equation true. This is based on the Zero Product Property, which states that if the product of two or more factors is zero, then at least one of the factors must be zero.For example, to solve the equation x 2
4x = 0, we first factor out the GCF, which is x
x(x
4) = 0
Now, we have two factors: x and (x
- 4). According to the Zero Product Property, either x = 0 or (x
- 4) = 0. Solving for x, we get x = 0 or x = 4. These are the solutions to the equation x 2
- 4x = 0.
6. Quadratic Equations and Functions
Quadratic equations and functions are an important part of algebra, and they have many real-world applications. In this section, we will explore the properties of quadratic equations, learn how to solve them, and understand the relationship between quadratic equations and their graphs.
Standard Form and Parabola
The standard form of a quadratic equation is given by `ax² + bx + c = 0`, where `a`, `b`, and `c` are real numbers and `a ≠ 0`. The graph of a quadratic equation is a parabola, which is a symmetrical curve that opens either upwards or downwards.The coefficients `a`, `b`, and `c` in the standard form influence the shape and position of the parabola.* Coefficient `a`: Determines the direction of the parabola’s opening.
If `a > 0`, the parabola opens upwards, and if `a < 0`, the parabola opens downwards. The absolute value of `a` also affects the width of the parabola. A larger value of `|a|` results in a narrower parabola, and a smaller value of `|a|` results in a wider parabola. - Coefficient `b`: Affects the horizontal position of the parabola. The vertex of the parabola, which is the lowest or highest point on the curve, is shifted horizontally by `-b/2a` units.
Coefficient `c`
Determines the vertical position of the parabola. The constant term `c` represents the y-intercept of the parabola, which is the point where the parabola intersects the y-axis.For example, consider the quadratic equation `y = x²
- 2x + 1`. The coefficient `a` is 1, so the parabola opens upwards. The coefficient `b` is
- 2, so the vertex is shifted 1 unit to the right. The coefficient `c` is 1, so the y-intercept is at the point (0, 1).
| Characteristic | Description |
|---|---|
| Vertex | The lowest or highest point on the parabola, located at `x =
|
| Axis of Symmetry | A vertical line passing through the vertex, dividing the parabola into two symmetrical halves. |
| Y-intercept | The point where the parabola intersects the y-axis, located at `(0, c)`. |
| X-intercepts | The points where the parabola intersects the x-axis, also known as the roots or zeros of the equation. |
| Direction of Opening | Determined by the sign of `a`. If `a > 0`, the parabola opens upwards, and if `a < 0`, the parabola opens downwards. |
Solving Quadratic Equations
Solving a quadratic equation means finding the values of `x` that satisfy the equation. There are several methods for solving quadratic equations, including factoring, the quadratic formula, and completing the square.
Factoring
Factoring is a method of solving quadratic equations by expressing the quadratic expression as a product of two linear factors. To factor a quadratic equation, we need to find two numbers that multiply to give `c` and add up to `b`.
Once we find these numbers, we can write the quadratic equation as a product of two linear factors, and then set each factor equal to zero to solve for `x`.For example, consider the quadratic equation `x²
- 5x + 6 = 0`. We need to find two numbers that multiply to give 6 and add up to
- 5. These numbers are
- 2 and
- So, we can factor the equation as follows:
`(x
- 2)(x
- 3) = 0`
Setting each factor equal to zero, we get:`x
Algebra 1 Honors is all about building a strong foundation in equations, inequalities, and functions. You’ll learn to solve complex problems, manipulate variables, and understand the relationships between different mathematical concepts. It’s a lot to take in, but it’s worth it – mastering these skills can open up doors to higher-level math courses and even careers in STEM fields.
Just like learning algebra, figuring out how long it takes to learn Portuguese depends on your dedication and learning style. How long does it take to learn Portuguese is a question with no single answer, but the same dedication and practice you put into algebra will pay off in your language learning journey too! So, keep at it, and you’ll be solving equations and speaking Portuguese in no time!
- 2 = 0` or `x
- 3 = 0`
Solving for `x`, we get:`x = 2` or `x = 3`
Quadratic Formula
The quadratic formula is a general solution for quadratic equations, and it can be used to solve any quadratic equation. The quadratic formula is derived by completing the square and is given by:
`x = (-b ± √(b²
4ac)) / 2a`
where `a`, `b`, and `c` are the coefficients of the quadratic equation.To use the quadratic formula, we simply substitute the values of `a`, `b`, and `c` into the formula and simplify.For example, consider the quadratic equation `2x² + 5×3 = 0`.
Here, `a = 2`, `b = 5`, and `c =
-3`. Substituting these values into the quadratic formula, we get
`x = (-5 ± √(5²
- 4
- 2
- 3)) / (2
- 2)`
Simplifying, we get:`x = (-5 ± √49) / 4`Therefore, the solutions to the quadratic equation are:`x = (-5 + 7) / 4 = 1/2` or `x = (-5
- 7) / 4 =
- 3`
Completing the Square
Completing the square is a method of solving quadratic equations by manipulating the equation to make one side a perfect square trinomial. To complete the square, we first move the constant term to the right side of the equation. Then, we take half of the coefficient of the `x` term, square it, and add it to both sides of the equation.
This will create a perfect square trinomial on the left side of the equation.For example, consider the quadratic equation `x²
6x + 5 = 0`. To complete the square, we first move the constant term to the right side of the equation
`x²
- 6x =
- 5`
Next, we take half of the coefficient of the `x` term, which is
-6, square it, which is 9, and add it to both sides of the equation
`x²
- 6x + 9 =
- 5 + 9`
This creates a perfect square trinomial on the left side of the equation:`(x
3)² = 4`
Taking the square root of both sides, we get:`x
3 = ±2`
Solving for `x`, we get:`x = 3 ± 2`Therefore, the solutions to the quadratic equation are:`x = 5` or `x = 1`
Discriminant and Nature of Solutions
The discriminant of a quadratic equation is given by `b²4ac`, where `a`, `b`, and `c` are the coefficients of the quadratic equation. The discriminant tells us about the nature of the solutions to the quadratic equation.* Positive Discriminant: If the discriminant is positive, the quadratic equation has two distinct real solutions.
This means that the parabola intersects the x-axis at two distinct points.
Zero Discriminant
If the discriminant is zero, the quadratic equation has one real solution, which is a double root. This means that the parabola intersects the x-axis at one point, which is the vertex of the parabola.
Negative Discriminant
If the discriminant is negative, the quadratic equation has two complex solutions. This means that the parabola does not intersect the x-axis.For example, consider the quadratic equation `x²
- 4x + 4 = 0`. The discriminant is `(-4)²
- 4
- 1
- 4 = 0`. Since the discriminant is zero, the quadratic equation has one real solution, which is a double root. The parabola intersects the x-axis at the point (2, 0), which is the vertex of the parabola.
Writing Prompts
- Write a step-by-step guide for solving a quadratic equation using the quadratic formula, including a clear explanation of each step and an example problem.
- Compare and contrast the methods of factoring, the quadratic formula, and completing the square for solving quadratic equations. Discuss the advantages and disadvantages of each method.
- Analyze the discriminant of a given quadratic equation and determine the nature of its solutions. Explain your reasoning and provide a visual representation of the parabola.
7. Exponential and Logarithmic Functions
Exponential and logarithmic functions are essential tools in mathematics, offering a way to model and understand various real-world phenomena. They are closely intertwined, with logarithmic functions serving as the inverse of exponential functions. This means they have a unique relationship, allowing us to solve equations and analyze growth and decay processes effectively.
Defining and Exploring Exponential Functions
Exponential functions are defined by a specific form,
- f(x) = a^x*, where
- a* represents the base and
- x* is the exponent. The base,
- a*, must be a positive constant, and the exponent,
- x*, can be any real number.
For example,
- f(x) = 2^x* is an exponential function with a base of 2. This function grows rapidly as
- x* increases. On the other hand,
- f(x) = (1/2)^x* is an exponential function with a base of 1/2. This function decays as
- x* increases.
- Exponential Growth: Exponential growth occurs when the value of a function increases rapidly over time. This happens when the base, -a*, is greater than 1. The larger the base, the faster the growth. For instance, the growth of a population or the spread of a virus can be modeled using exponential growth functions.
- Exponential Decay: Exponential decay occurs when the value of a function decreases rapidly over time. This happens when the base, -a*, is between 0 and 1. The smaller the base, the faster the decay. Examples of exponential decay include radioactive decay, the depreciation of an asset, or the cooling of a hot object.
Properties of Exponential Functions
Exponential functions have distinct properties that define their behavior.
- Domain and Range: The domain of an exponential function is all real numbers, meaning that -x* can take any value. The range, however, depends on the base. For exponential functions with a base greater than 1, the range is all positive real numbers.
For exponential functions with a base between 0 and 1, the range is all positive real numbers less than 1.
- Asymptotes: Exponential functions have a horizontal asymptote. For functions with a base greater than 1, the horizontal asymptote is the x-axis (y = 0). For functions with a base between 0 and 1, the horizontal asymptote is also the x-axis (y = 0).
- Growth or Decay: As mentioned earlier, exponential functions with a base greater than 1 exhibit growth, while those with a base between 0 and 1 exhibit decay.
- Transformations: Exponential functions can be transformed by shifting, stretching, or reflecting their graphs. A vertical shift is achieved by adding a constant to the function. A horizontal shift is achieved by adding a constant to the exponent. A vertical stretch is achieved by multiplying the function by a constant.
A horizontal stretch is achieved by multiplying the exponent by a constant. A reflection about the y-axis is achieved by negating the exponent.
Graphs of Exponential Functions
The graph of an exponential function has a distinctive shape, characterized by its rapid growth or decay.
- General Shape: The graph of an exponential function with a base greater than 1 increases rapidly as -x* increases. It starts slowly, then grows more quickly. The graph of an exponential function with a base between 0 and 1 decreases rapidly as -x* increases.
It starts high and then decays quickly.
- Effect of Base: Changing the base affects the steepness of the graph. A larger base results in a steeper graph, indicating faster growth or decay. A smaller base results in a less steep graph, indicating slower growth or decay.
- Effect of Exponent: Changing the exponent affects the rate of growth or decay. A larger exponent results in faster growth or decay. A smaller exponent results in slower growth or decay.
Understanding Logarithmic Functions, What do you learn in algebra 1 honors
Logarithmic functions are the inverse of exponential functions. They are defined by the equation
- log_a(x) = y*, where
- a* is the base,
- x* is the argument, and
- y* is the exponent. This means that the logarithm of a number
- x* to the base
- a* is the exponent to which
- a* must be raised to obtain
- x*.
For example,log_2(8) = 3* because 2 raised to the power of 3 equals 8. In other words, the logarithmic function “undoes” the exponential function.
Properties of Logarithmic Functions
Logarithmic functions have properties that are closely related to those of exponential functions.
- Domain and Range: The domain of a logarithmic function is all positive real numbers. The range is all real numbers. This is the opposite of the domain and range of the corresponding exponential function.
- Asymptotes: Logarithmic functions have a vertical asymptote. The vertical asymptote is the y-axis (x = 0).
- Relationship to Exponential Functions: The base of the logarithmic function is the same as the base of the corresponding exponential function. This means that -log_a(x)* is the inverse of -a^x*.
- Transformations: Logarithmic functions can also be transformed by shifting, stretching, or reflecting their graphs. These transformations are similar to those for exponential functions, with the key difference being that horizontal transformations are applied to the argument of the logarithmic function, while vertical transformations are applied to the function itself.
Graphs of Logarithmic Functions
The graph of a logarithmic function has a distinctive shape that is the reflection of the graph of the corresponding exponential function.
- General Shape: The graph of a logarithmic function with a base greater than 1 increases slowly as -x* increases. It starts high and then grows more slowly. The graph of a logarithmic function with a base between 0 and 1 decreases slowly as -x* increases.
It starts low and then decays more slowly.
- Effect of Base: Changing the base affects the steepness of the graph. A larger base results in a less steep graph, indicating slower growth or decay. A smaller base results in a steeper graph, indicating faster growth or decay. This is the opposite of the effect of changing the base on the graph of an exponential function.
- Effect of Argument: Changing the argument of a logarithmic function affects the horizontal position of the graph. A larger argument shifts the graph to the right, while a smaller argument shifts the graph to the left.
Connecting Exponential and Logarithmic Functions
Exponential and logarithmic functions are inextricably linked. Their inverse relationship is fundamental to understanding and solving equations involving these functions.
- Inverse Relationship: The exponential function -a^x* and the logarithmic function -log_a(x)* are inverses of each other. This means that if -y = a^x*, then -x = log_a(y)*. This relationship is illustrated by the fact that the graphs of -y = a^x* and -y = log_a(x)* are reflections of each other about the line -y = x*.
- Logarithmic and Exponential Identities: The inverse relationship between exponential and logarithmic functions leads to several important identities. For example, -log_a(a^x) = x* and -a^(log_a(x)) = x*. These identities are useful for simplifying expressions and solving equations.
Solving Equations
The inverse relationship between exponential and logarithmic functions is essential for solving equations involving these functions.
- Solving Exponential Equations: To solve an exponential equation, we can use the logarithmic function to isolate the exponent. For example, to solve the equation -2^x = 8*, we can take the logarithm of both sides with base 2: -log_2(2^x) = log_2(8)*.
Using the identity -log_a(a^x) = x*, we get -x = log_2(8) = 3*.
- Solving Logarithmic Equations: To solve a logarithmic equation, we can use the exponential function to isolate the argument. For example, to solve the equation -log_2(x) = 3*, we can exponentiate both sides with base 2: -2^(log_2(x)) = 2^3*. Using the identity -a^(log_a(x)) = x*, we get -x = 2^3 = 8*.
8. Inequalities and Systems of Inequalities
Inequalities are mathematical statements that compare two expressions using symbols like <, >, ≤, or ≥. They are essential for representing situations involving constraints, limitations, or ranges of values. This section delves into linear inequalities in one and two variables, and systems of inequalities, exploring how to solve and represent their solutions graphically.
Linear Inequalities in One Variable
Solving linear inequalities in one variable involves finding the set of values that satisfy the inequality. The process is similar to solving equations, but with one crucial difference: multiplying or dividing both sides of the inequality by a negative number requires flipping the inequality sign.
Solving Linear Inequalities in One Variable
- Example:Solve the inequality 2x + 5 > 11.
- Step 1:Subtract 5 from both sides: 2x > 6.
- Step 2:Divide both sides by 2: x > 3.
- Solution:The solution to the inequality is x > 3, which means all values of x greater than 3 satisfy the inequality.
- Representing the Solution on a Number Line:A number line can visually represent the solution set. An open circle at 3 indicates that 3 is not included in the solution set, and a shaded line extending to the right represents all values greater than 3.
Difference between Solving Equations and Inequalities
- Equations:Solving equations involves finding a specific value that makes the equation true. For example, the equation 2x + 5 = 11 has a solution of x = 3.
- Inequalities:Solving inequalities involves finding a range of values that satisfy the inequality. For example, the inequality 2x + 5 > 11 has a solution set of x > 3.
- Key Difference:When multiplying or dividing both sides of an inequality by a negative number, the inequality sign must be flipped. This is not necessary when solving equations.
Linear Inequalities in Two Variables
Linear inequalities in two variables involve two variables (usually x and y) and a comparison using inequality symbols. Graphing the solution set of such inequalities requires understanding the concept of a boundary line and choosing a test point to determine the shaded region.
Graphing Linear Inequalities in Two Variables
- Example:Graph the solution set of the inequality y < 2x - 3.
- Step 1:Graph the boundary line: The boundary line is obtained by replacing the inequality symbol ( <) with an equals sign (=). In this case, the boundary line is y = 2x - 3. This line is dashed because the inequality does not include the points on the line itself.
- Step 2:Choose a test point: Select a point that does not lie on the boundary line. For example, the point (0,0) is a good choice.
- Step 3:Substitute the test point into the inequality: Substituting (0,0) into y < 2x - 3 gives 0 < -3, which is false.
- Step 4:Shade the appropriate region: Since the test point (0,0) did not satisfy the inequality, the region on the opposite side of the boundary line from the test point is shaded. In this case, the region below the boundary line is shaded.
Boundary Line in Graphing Linear Inequalities
The boundary line represents the points that satisfy the equation obtained by replacing the inequality symbol with an equals sign. It separates the coordinate plane into two regions.
- Inequalities with “less than” (<) or "less than or equal to" (≤):The shaded region lies below the boundary line.
- Inequalities with “greater than” (>) or “greater than or equal to” (≥):The shaded region lies above the boundary line.
Systems of Inequalities
A system of inequalities consists of two or more inequalities that are considered simultaneously. The solution set of a system of inequalities is the set of all points that satisfy all the inequalities in the system.
Finding the Solution Set of a System of Inequalities Graphically
- Example:Consider the system of inequalities:
- y < 2x - 3
- x + y ≤ 4
- Step 1:Graph each inequality separately: Graph the first inequality (y < 2x - 3) as explained in the previous section. Then, graph the second inequality (x + y ≤ 4) by following the same steps, noting that the boundary line is solid because the inequality includes the points on the line.
- Step 2:Identify the intersection: The solution set of the system of inequalities is the region where the shaded regions of both inequalities overlap. This overlapping region is the solution set because it represents the points that satisfy both inequalities.
Interpreting the Solution Set in Real-World Scenarios
Systems of inequalities can model real-world situations involving constraints or limitations. The solution set represents the feasible region, which is the set of all possible solutions that satisfy the given constraints.
- Example:A bakery produces two types of cakes, chocolate and vanilla. Each chocolate cake requires 2 cups of flour and 1 cup of sugar, while each vanilla cake requires 1 cup of flour and 2 cups of sugar. The bakery has 10 cups of flour and 8 cups of sugar available.
To model this situation, we can use a system of inequalities:
- 2x + y ≤ 10 (flour constraint)
- x + 2y ≤ 8 (sugar constraint)
where x represents the number of chocolate cakes and y represents the number of vanilla cakes. The solution set of this system represents the combinations of chocolate and vanilla cakes that the bakery can produce using the available resources.
Feasible Region in Systems of Inequalities
The feasible region is the solution set of a system of inequalities. It represents the set of all points that satisfy all the constraints in the system. In real-world applications, the feasible region often represents the set of possible solutions or outcomes that are achievable within the given limitations.
- Example:In the bakery example above, the feasible region represents the combinations of chocolate and vanilla cakes that the bakery can produce given the limited resources. The points within the feasible region represent feasible production plans.
Writing Prompts
- Word Problem:A local farmer wants to plant two types of crops, corn and soybeans. Each acre of corn requires 20 hours of labor and 10 gallons of fertilizer, while each acre of soybeans requires 10 hours of labor and 20 gallons of fertilizer.
The farmer has a maximum of 100 hours of labor and 80 gallons of fertilizer available. Write a system of inequalities to model this situation and graph the solution set.
- Explanation for a Friend:Imagine you are explaining the concept of systems of inequalities to a friend who is unfamiliar with the topic. Write a clear and concise explanation that includes examples and visuals. For instance, you could use the bakery example above to illustrate how systems of inequalities can be used to represent real-world situations involving constraints.
Rational Expressions and Equations: What Do You Learn In Algebra 1 Honors
Rational expressions are algebraic expressions that can be written as a fraction where the numerator and denominator are polynomials. These expressions are fundamental in algebra, especially when dealing with complex equations and functions. Understanding how to simplify, manipulate, and solve rational expressions is crucial for solving various real-world problems.
Simplifying Rational Expressions
Simplifying rational expressions involves reducing them to their simplest form by canceling out common factors in the numerator and denominator. To simplify a rational expression, follow these steps:
- Factor both the numerator and denominator completely.
- Identify any common factors in the numerator and denominator.
- Cancel out the common factors.
For example, consider the rational expression:
(x^2
4) / (x + 2)
- Factoring the numerator, we get (x + 2)(x – 2)
- The expression becomes: (x + 2)(x – 2) / (x + 2)
- Canceling out the common factor (x + 2), we are left with: (x – 2)
Therefore, the simplified form of the rational expression (x^2
- 4) / (x + 2) is (x
- 2).
Performing Operations on Rational Expressions
Rational expressions can be added, subtracted, multiplied, and divided just like ordinary fractions.
Addition and Subtraction
To add or subtract rational expressions, they must have a common denominator. If they don’t, you need to find the least common multiple (LCM) of the denominators and rewrite each expression with the LCM as the denominator.For example, consider adding the following rational expressions:
(x + 1) / (x
- 2) + (x
- 3) / (x + 1)
- The LCM of the denominators is (x – 2)(x + 1)
- Rewrite the first expression: [(x + 1)(x + 1)] / [(x – 2)(x + 1)]
- Rewrite the second expression: [(x – 3)(x – 2)] / [(x – 2)(x + 1)]
- Adding the numerators: [(x + 1)(x + 1) + (x – 3)(x – 2)] / [(x – 2)(x + 1)]
- Simplifying the numerator: (2x^2 – 2x – 5) / [(x – 2)(x + 1)]
Therefore, the sum of the two rational expressions is (2x^2
- 2x
- 5) / [(x
- 2)(x + 1)].
Multiplication
To multiply rational expressions, multiply the numerators and the denominators.For example, consider multiplying the following rational expressions:
(x^2
- 9) / (x + 3)
- (x + 2) / (x
- 3)
- Multiply the numerators: (x^2 – 9)(x + 2)
- Multiply the denominators: (x + 3)(x – 3)
- Simplify the expression: [(x + 3)(x – 3)(x + 2)] / [(x + 3)(x – 3)]
- Cancel out the common factors: (x + 2)
Therefore, the product of the two rational expressions is (x + 2).
Division
To divide rational expressions, invert the second expression and multiply.For example, consider dividing the following rational expressions:
(x^2
- 4) / (x
- 2) ÷ (x + 2) / (x
- 1)
- Invert the second expression: (x – 1) / (x + 2)
- Multiply the first expression by the inverted second expression: [(x^2 – 4) / (x – 2)] – [(x – 1) / (x + 2)]
- Simplify the expression: [(x + 2)(x – 2)(x – 1)] / [(x – 2)(x + 2)]
- Cancel out the common factors: (x – 1)
Therefore, the quotient of the two rational expressions is (x
1).
Solving Rational Equations
Solving rational equations involves finding the values of the variable that make the equation true. To solve a rational equation, follow these steps:
- Find the least common multiple (LCM) of the denominators.
- Multiply both sides of the equation by the LCM to eliminate the fractions.
- Solve the resulting equation.
- Check for extraneous solutions.
Extraneous solutions are values that satisfy the simplified equation but do not satisfy the original equation. They arise when the original equation has restrictions on the domain, such as values that make the denominator zero.For example, consider the rational equation:
- / (x
- 2) + 2 / (x + 1) = 3 / (x
- 2)
- The LCM of the denominators is (x – 2)(x + 1)
- Multiply both sides of the equation by (x – 2)(x + 1): (x + 1) + 2(x – 2) = 3(x + 1)
- Simplify and solve for x: x = 5
- Check for extraneous solutions. The original equation has restrictions on the domain: x ≠ 2 and x ≠ -1. Since x = 5 does not violate these restrictions, it is a valid solution.
Therefore, the solution to the rational equation is x = 5.
Radical Expressions and Equations
In Algebra 1 Honors, you’ll delve into the world of radical expressions and equations, which involve roots, particularly square roots. This unit builds upon your understanding of exponents and introduces new concepts that are essential for solving various mathematical problems.
Simplifying Radical Expressions
Simplifying radical expressions involves rewriting them in their simplest form. This process utilizes the properties of radicals and the concept of prime factorization.
The main property of radicals states that the square root of a product is equal to the product of the square roots: √(ab) = √a
√b.
To simplify a radical expression, you follow these steps:
- Factor out any perfect squares from the radicand (the number under the radical sign).
- Take the square root of the perfect square, and leave the remaining factors under the radical.
For example, to simplify √48, you would factor 48 as 16
- 3. Since 16 is a perfect square, you can rewrite √48 as √(16
- 3) = √16
- √3 = 4√3.
Operations on Radical Expressions
You can perform various operations on radical expressions, including addition, subtraction, multiplication, and division.
When adding or subtracting radical expressions, the radicands must be the same.
For instance, 2√5 + 3√5 = 5√5. However, 2√5 + 3√2 cannot be simplified further.
When multiplying or dividing radical expressions, you can multiply or divide the radicands and the coefficients separately.
For example, (2√3)
(5√2) = 10√6, and (√12) / (√3) = √(12/3) = √4 = 2.
Solving Radical Equations
Radical equations are equations that contain radical expressions with variables. To solve them, you need to isolate the radical term and then square both sides of the equation. This eliminates the radical sign.
When squaring both sides of an equation, remember to check for extraneous solutions. These are solutions that arise from the squaring process but do not satisfy the original equation.
For example, consider the equation √(x + 2) = 3. Squaring both sides gives x + 2 = 9. Solving for x yields x = 7. However, you must check if x = 7 satisfies the original equation. Plugging it in, you get √(7 + 2) = √9 = 3, which confirms that x = 7 is a valid solution.
Sequences and Series
Sequences and series are fundamental concepts in mathematics that involve patterns and sums. A sequence is a list of numbers arranged in a specific order, while a series is the sum of the terms in a sequence. Understanding sequences and series allows you to model various real-world phenomena, from population growth to compound interest.
Arithmetic Sequences
An arithmetic sequence is a sequence where the difference between consecutive terms is constant. This constant difference is called the common difference.
An arithmetic sequence can be represented by the formula: an= a 1+ (n
1)d
Where:
- a nis the nth term
- a 1is the first term
- d is the common difference
- n is the number of terms
For example, the sequence 2, 5, 8, 11, 14… is an arithmetic sequence with a common difference of 3.
Geometric Sequences
A geometric sequence is a sequence where the ratio between consecutive terms is constant. This constant ratio is called the common ratio.
A geometric sequence can be represented by the formula: an= a 1
r(n-1)
Where:
- a nis the nth term
- a 1is the first term
- r is the common ratio
- n is the number of terms
For example, the sequence 2, 6, 18, 54, 162… is a geometric sequence with a common ratio of 3.
Series
A series is the sum of the terms in a sequence.
The sum of a finite arithmetic series is: Sn= n/2
(a1+ a n)
Where:
- S nis the sum of the first n terms
- a 1is the first term
- a nis the nth term
- n is the number of terms
The sum of a finite geometric series is: Sn= a 1
- (1
- r n) / (1
- r)
Where:
- S nis the sum of the first n terms
- a 1is the first term
- r is the common ratio
- n is the number of terms
The sum of an infinite geometric series is: S∞= a 1/ (1
r)
Where:
- S ∞is the sum of the infinite series
- a 1is the first term
- r is the common ratio
This formula is only valid if the absolute value of the common ratio is less than 1 (|r| < 1).
Applications of Sequences and Series
Sequences and series have numerous applications in various fields, including:
Finance
Calculating compound interest and loan payments.
Physics
Modeling the motion of objects and the decay of radioactive materials.
Biology
Studying population growth and the spread of diseases.
Computer science
Analyzing algorithms and data structures.For example, the formula for compound interest is based on a geometric series. The formula for the present value of an annuity also relies on the concept of geometric series.
Data Analysis and Statistics
Data analysis is the process of examining raw data to extract meaningful insights and patterns. It plays a crucial role in decision-making across various fields, from business and finance to science and healthcare. By understanding data, we can identify trends, make predictions, and draw conclusions that inform strategic choices.
Types of Data
Data can be broadly classified into two categories: quantitative and qualitative.
- Quantitative datais numerical and can be measured. Examples include height, weight, age, and income.
- Qualitative datais descriptive and deals with qualities or characteristics. Examples include color, texture, taste, and opinions.
Measures of Central Tendency
Measures of central tendency are statistical values that represent the typical or average value in a dataset. They help us understand the central location of the data.
- Mean:The average of all values in a dataset. It is calculated by summing all values and dividing by the total number of values.
Mean = (Sum of all values) / (Total number of values)
- Median:The middle value in a sorted dataset. If the dataset has an even number of values, the median is the average of the two middle values.
- Mode:The value that appears most frequently in a dataset. A dataset can have multiple modes or no mode at all.
13. Probability and Statistics
Probability and statistics are essential tools for understanding and interpreting data in various fields. They help us quantify the likelihood of events, analyze trends, and make informed decisions based on available information. This section explores the fundamental concepts of probability and statistics, including their calculation methods, applications in real-world scenarios, and the significance of understanding these concepts in our daily lives.
Probability and Calculation Methods
Probability is a measure of the likelihood of an event occurring. It is expressed as a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. Higher probability values indicate a greater likelihood of the event occurring.There are three main methods for calculating probability:
- Classical Probability:This method applies when all outcomes of an event are equally likely. The probability of an event is calculated by dividing the number of favorable outcomes by the total number of possible outcomes. For example, when rolling a fair die, the probability of getting a 6 is 1/6, as there is one favorable outcome (rolling a 6) and six possible outcomes (rolling 1, 2, 3, 4, 5, or 6).
- Empirical Probability:This method is based on observed data or experiments. The probability of an event is calculated by dividing the number of times the event occurred by the total number of trials. For example, if a coin is flipped 100 times and lands on heads 55 times, the empirical probability of getting heads is 55/100 = 0.55.
- Subjective Probability:This method relies on personal beliefs or judgments. It is often used when there is limited or no objective data available. For example, if you are asked to estimate the probability of your favorite team winning a sports game, you might base your answer on your knowledge of the teams’ performance, the players’ abilities, and other factors.
Independent and Dependent Events
Events are considered independent if the outcome of one event does not affect the outcome of another event. For example, flipping a coin and rolling a die are independent events, as the result of the coin flip does not influence the outcome of the die roll.Events are considered dependent if the outcome of one event influences the outcome of another event.
For example, drawing two cards from a deck without replacement is a dependent event, as the outcome of the first draw affects the probability of the second draw.
Real-World Applications of Probability and Statistics
Probability and statistics are widely used in various fields, including:
- Insurance:Insurance companies use probability to calculate premiums and assess risk. They estimate the likelihood of insured events occurring, such as accidents or illnesses, and adjust premiums accordingly.
- Quality Control:Statistical methods are used in quality control to monitor and improve product quality. By analyzing data on product defects, companies can identify areas for improvement and reduce production costs.
- Market Research:Probability and statistics are used in market research to analyze data and make predictions about consumer behavior. Companies can use this information to develop effective marketing campaigns and target specific customer segments.
- Medical Research:Statistics play a crucial role in medical research, including hypothesis testing and data analysis. Researchers use statistical methods to analyze clinical trial data and draw conclusions about the effectiveness of new treatments.
Essay on Probability and Statistics
Probability and statistics are fundamental tools for understanding and interpreting data in our complex world. Probability allows us to quantify the likelihood of events, helping us make informed decisions and manage risk. Statistics provide methods for analyzing data, identifying trends, and drawing meaningful conclusions.Probability is essential in various aspects of our lives.
From weather forecasting to financial markets, probability helps us predict future outcomes based on past data and current conditions. Insurance companies rely on probability to calculate premiums and assess risk, ensuring that they can cover potential losses. In healthcare, probability is used to determine the effectiveness of treatments and assess the risk of complications.Statistics are equally important in our daily lives.
We encounter statistical data in news reports, scientific studies, and marketing campaigns. Understanding statistical concepts helps us critically evaluate information, identify biases, and make informed decisions. For example, when reading about a new health study, it is essential to understand the statistical methods used and the sample size to determine the validity of the findings.In conclusion, probability and statistics are essential tools for understanding and interpreting data in various fields.
They help us quantify the likelihood of events, analyze trends, and make informed decisions based on available information. By understanding these concepts, we can make better decisions, manage risk effectively, and navigate our complex world with greater confidence.
Problem-Solving and Applications

Algebra isn’t just about manipulating symbols; it’s a powerful tool for understanding and solving real-world problems. This section explores how algebraic concepts can be applied to various situations.
Translating Word Problems into Equations
Algebraic equations are essentially mathematical representations of real-world scenarios. Learning to translate word problems into equations is crucial for applying algebra to solve practical problems. Here’s a step-by-step guide to translate word problems into equations:* Identify the unknowns:Determine the variables you need to represent in the problem.
For example, if a problem asks for the cost of a book, you might use the variable ‘x’ to represent the unknown cost.
Represent the relationships
Analyze the problem and identify the relationships between the unknowns. For example, if the problem states that the cost of two books is $20, you can represent this relationship as ‘2x = 20’.
Write the equation
Combine the relationships you’ve identified to form an equation. The equation should accurately reflect the problem’s context.
For example, consider the problem: “A store sells apples for $1.50 each and oranges for $0.75 each. If you buy 3 apples and 2 oranges, how much will it cost?”To solve this problem, you can use the following steps:
1. Identify the unknowns
The unknowns are the total cost of the apples (let’s call it ‘a’) and the total cost of the oranges (let’s call it ‘o’).
2. Represent the relationships
The cost of the apples is the price per apple multiplied by the number of apples: a = 1.50
- Similarly, the cost of the oranges is the price per orange multiplied by the number of oranges: o = 0.75
2. 3. Write the equation
The total cost is the sum of the cost of the apples and the cost of the oranges: Total cost = a + o. Substituting the expressions we found for ‘a’ and ‘o’, we get: Total cost = (1.50
- 3) + (0.75
- 2).
Solving Real-World Problems with Algebra
Algebraic concepts are widely used in various fields, including:* Finance:Calculating interest, loan repayments, and investment returns.
Science
Formulating and solving equations to model physical phenomena.
Engineering
Designing structures, analyzing forces, and optimizing systems.
Business
Predicting sales, analyzing costs, and optimizing production.Here are some examples of real-world problems that can be solved using algebraic concepts:* Calculating the distance traveled:If a car travels at a constant speed of 60 miles per hour for 3 hours, you can use the formula ‘distance = speedtime’ to calculate the distance traveled.
Determining the amount of paint needed
If you need to paint a room with a specific area, you can use the formula ‘area = length
- width’ to calculate the area and then use the paint coverage information to determine the amount of paint needed.
Finding the optimal investment strategy
You can use algebraic equations to model different investment scenarios and determine the best strategy based on your financial goals and risk tolerance.
Popular Questions
What are the benefits of taking Algebra 1 Honors?
Algebra 1 Honors offers a deeper understanding of algebraic concepts and prepares you for more advanced math courses. It also demonstrates your commitment to academic excellence and can boost your college applications.
Is Algebra 1 Honors harder than regular Algebra 1?
Yes, Algebra 1 Honors typically covers more material at a faster pace and expects a higher level of understanding and problem-solving skills.
What kind of homework can I expect in Algebra 1 Honors?
Expect a significant amount of homework, including practice problems, concept-based questions, and possibly projects or presentations.
What resources are available to help me succeed in Algebra 1 Honors?
Your teacher, textbook, online resources, study groups, and tutoring services can all be valuable resources for success in Algebra 1 Honors.