Is Q-learning provably efficient? This question has captivated researchers in the field of reinforcement learning for years. Q-learning, a powerful algorithm that enables agents to learn optimal strategies through trial and error, has revolutionized how we approach complex decision-making problems.
But can we definitively say that Q-learning is guaranteed to find the best solution, and if so, how quickly? This exploration delves into the theoretical and practical aspects of Q-learning efficiency, examining its strengths, limitations, and the exciting possibilities for its future.
Q-learning stands out as a model-free, off-policy algorithm, meaning it doesn’t require a predefined model of the environment and can learn from any sequence of actions and rewards. This flexibility makes it adaptable to a wide range of real-world scenarios, from game playing to robotics and even healthcare.
At its core, Q-learning learns by constructing a Q-table, a data structure that maps state-action pairs to their expected future rewards. By repeatedly updating these Q-values based on experience, the agent gradually refines its strategy, ultimately aiming to maximize its cumulative reward.
1. Introduction to Q-Learning

Q-learning is a powerful reinforcement learning algorithm that enables agents to learn optimal policies by interacting with their environment. It’s a cornerstone of artificial intelligence, finding applications in diverse domains like robotics, game playing, and autonomous driving.
1.1 Defining Q-learning and its role in reinforcement learning
Reinforcement learning is a type of machine learning where an agent learns to interact with an environment to maximize cumulative rewards. The core principles of reinforcement learning involve:
Agent
An entity that interacts with the environment.
Environment
The external world that the agent interacts with.
State
A snapshot of the environment at a particular moment.
Action
An action that the agent can take in a given state.
Reward
A numerical value that reflects the desirability of a particular state or action.Q-learning stands out as a model-free, off-policyreinforcement learning algorithm. This means that it doesn’t require a model of the environment to learn and can learn from experiences even if the agent isn’t following the optimal policy.
Q-learning learns from experience by iteratively updating its knowledge of the environment and refining its decision-making. This continuous learning process allows the agent to improve its performance over time.
1.2 Value functions and their relation to Q-learning
Value functions are central to reinforcement learning. They quantify the expected future rewards associated with different states or actions. There are two types of value functions:
State-value function (V(s))
Represents the expected cumulative reward for starting in state ‘s’ and following a particular policy.
Action-value function (Q(s, a))
Represents the expected cumulative reward for taking action ‘a’ in state ‘s’ and following a particular policy afterward.Q-learning utilizes action-value functions, often called Q-values, to estimate the expected future rewards for taking specific actions in given states. The goal of Q-learning is to learn the optimal Q-value for each state-action pair.
1.3 Key components of a Q-learning algorithm
Q-learning relies on four key components:
State (s)
The current situation or configuration of the environment.
Action (a)
The action the agent chooses to take in the current state.
Reward (r)
The immediate reward received by the agent for taking action ‘a’ in state ‘s’.
Q-table
A table that stores and updates Q-values for different state-action pairs. The Q-table is essentially a lookup table where each row represents a state, each column represents an action, and each cell contains the estimated Q-value for that state-action pair.The Q-learning update rule, which is used to update the Q-values in the Q-table, involves two key parameters:
Learning rate (α)
Controls the influence of new experiences on the Q-value updates. A higher learning rate gives more weight to recent experiences, while a lower learning rate gives more weight to past experiences.
Discount factor (γ)
Determines the importance of future rewards compared to immediate rewards. A higher discount factor emphasizes future rewards, while a lower discount factor emphasizes immediate rewards.
1.4 Summary of Q-learning
Q-learning is a model-free, off-policy reinforcement learning algorithm that learns the optimal policy by iteratively updating the Q-values in a Q-table. It estimates the expected future rewards for taking specific actions in given states and uses these estimates to guide its decision-making.
Q-learning has the advantage of being able to learn from experience without requiring a model of the environment. However, it can be computationally expensive for large state and action spaces.Q-learning has found practical applications in diverse fields, including:
Game playing
Q-learning has been successfully used to train agents to play games like chess and Go.
Robotics
Q-learning can be used to train robots to perform tasks like navigating complex environments and manipulating objects.
Autonomous driving
Q-learning can be used to train self-driving cars to make decisions about lane changes, braking, and acceleration.
1.5 Simple Q-learning example
Let’s imagine a simple scenario where an agent is navigating a grid world. The agent’s goal is to reach a designated goal state while avoiding obstacles.
States
Each cell in the grid represents a state.
Actions
The agent can move up, down, left, or right.
Rewards
The agent receives a positive reward for reaching the goal state and a negative reward for hitting an obstacle.The Q-table will have rows representing each state and columns representing each action. Initially, the Q-values are set to zero.As the agent explores the grid world, it will encounter different states and actions.
For each state-action pair, the agent will update its Q-value using the Q-learning update rule. The agent will gradually learn to associate higher Q-values with actions that lead to the goal state and lower Q-values with actions that lead to obstacles.Over time, the agent’s policy will evolve based on the learned Q-values.
It will start to prefer actions that lead to higher rewards and avoid actions that lead to lower rewards. Eventually, the agent will learn to navigate the grid world efficiently and reach the goal state with minimal obstacles encountered.
The Efficiency of Q-Learning

In the realm of reinforcement learning, Q-learning stands out as a powerful algorithm for learning optimal policies. However, the effectiveness of Q-learning is not merely about achieving a good policy but also about how efficiently it learns. This efficiency is crucial, especially when dealing with complex environments with large state and action spaces.
Factors Influencing Efficiency
The efficiency of Q-learning is influenced by several factors. Understanding these factors helps us optimize the learning process and achieve faster convergence to optimal policies.
- Learning Rate: The learning rate, denoted by α, controls how much the Q-values are updated with each new experience. A higher learning rate leads to faster updates but can also cause instability if the rate is too high. Conversely, a lower learning rate promotes stability but can slow down the learning process.
The optimal learning rate is often determined through experimentation.
- Exploration Rate: The exploration rate, denoted by ε, determines the balance between exploring new actions and exploiting known actions. A higher exploration rate encourages exploration, allowing the agent to discover new and potentially better actions. However, excessive exploration can hinder learning, especially in environments with sparse rewards.
Conversely, a lower exploration rate focuses on exploiting known actions, leading to faster convergence but potentially missing optimal solutions. The exploration rate is typically decreased over time to shift the focus from exploration to exploitation.
- State and Action Space Size: The size of the state and action spaces significantly affects the complexity of the learning problem. Larger spaces require more memory to store Q-values and longer learning times to explore all possible combinations. Efficiently representing the state and action spaces is crucial for scaling Q-learning to complex environments.
Convergence in Q-Learning
Convergence in Q-learning refers to the process where the Q-values stabilize and converge to their optimal values. Convergence is a key indicator of efficiency, as it implies that the agent has learned a stable and optimal policy.
Convergence is achieved when the Q-values converge to their optimal values, meaning that the agent has learned a stable and optimal policy.
Several factors influence convergence, including the learning rate, exploration rate, and the structure of the environment. For instance, a properly chosen learning rate and exploration rate can accelerate convergence, while a complex environment with many states and actions can slow down the process.
3. Theoretical Bounds on Q-Learning Efficiency
Understanding the theoretical bounds on Q-learning’s efficiency is crucial for assessing its performance and guiding its practical application. These bounds provide insights into how quickly Q-learning converges to the optimal policy, under specific assumptions about the environment and the learning process.
Existing Bounds on Q-Learning Convergence Rate
Theoretical bounds on the convergence rate of Q-learning algorithms offer valuable insights into their efficiency. These bounds quantify the rate at which Q-learning converges to the optimal policy, under specific assumptions about the environment and the learning process. Here’s a table summarizing some of the most prominent bounds:
| Bound Name | Mathematical Expression | Assumptions | Key Insights |
|---|---|---|---|
| Jaksch et al. (2010) | ε(t) = O(1/t) | Finite state and action spaces, bounded rewards, and a specific exploration strategy | Guarantees convergence to the optimal policy at a rate of 1/t, where t is the number of iterations. |
| Even-Dar and Mansour (2003) | ε(t) = O(log(t)/t) | Finite state and action spaces, bounded rewards, and a specific exploration strategy | Provides a tighter bound than Jaksch et al., with a logarithmic dependence on the number of iterations. |
| Munos (2007) | ε(t) = O(1/sqrt(t)) | Finite state and action spaces, bounded rewards, and a specific exploration strategy | This bound highlights the potential for faster convergence compared to the previous bounds. |
Assumptions and Limitations
While these bounds provide valuable theoretical insights, they rely on specific assumptions that may not always hold in real-world applications. It’s essential to understand the limitations of these assumptions to interpret the bounds accurately and to guide the design of Q-learning algorithms.
Finite State and Action Spaces:Many theoretical bounds assume a finite state and action space, which may not be realistic in complex environments with continuous state and action spaces.
Bounded Rewards:The assumption of bounded rewards simplifies the analysis but may not be applicable in scenarios with unbounded rewards, such as financial markets.
Specific Exploration Strategies:The theoretical bounds often rely on specific exploration strategies, such as ε-greedy exploration, which may not be optimal in all scenarios.
Comparison of Theoretical Approaches
Different theoretical approaches have been employed to analyze Q-learning efficiency. Each approach has its strengths and weaknesses, influencing its applicability in different scenarios.
| Approach Name | Key Characteristics | Strengths | Weaknesses | Relevant References |
|---|---|---|---|---|
| Worst-Case Analysis | Focuses on the worst-case performance of Q-learning algorithms. | Provides guarantees on the convergence rate even in the most challenging scenarios. | May be overly pessimistic and not reflect the typical performance in real-world applications. | Jaksch et al. (2010), Even-Dar and Mansour (2003) |
| Average-Case Analysis | Analyzes the average performance of Q-learning algorithms over a set of environments. | Provides a more realistic assessment of performance compared to worst-case analysis. | Requires assumptions about the distribution of environments, which may not always be known. | Munos (2007) |
Empirical Evidence of Q-Learning Efficiency
While theoretical analysis provides insights into Q-learning’s potential, real-world applications and empirical studies offer concrete evidence of its efficiency. Numerous examples demonstrate Q-learning’s successful implementation in diverse domains, highlighting its practical value and effectiveness.
Real-World Applications of Q-Learning
Q-learning has proven its worth in various real-world scenarios, demonstrating its ability to learn and adapt in complex environments. Here are some notable examples:
- Game Playing:Q-learning has achieved remarkable success in game playing, particularly in the realm of Atari games. DeepMind’s groundbreaking work with Deep Q-Networks (DQN) demonstrated the ability of Q-learning to master complex Atari games, achieving human-level performance in many cases. This success highlights Q-learning’s capacity to learn optimal strategies in highly dynamic and challenging environments.
- Robotics:In robotics, Q-learning has been employed to train robots for tasks such as navigation, manipulation, and grasping. For instance, Q-learning has been used to develop robots that can learn to navigate complex environments autonomously, avoiding obstacles and reaching target locations.
Its ability to handle continuous state and action spaces makes it suitable for robotic applications.
- Finance:Q-learning has found applications in finance, particularly in algorithmic trading. By learning from historical market data, Q-learning algorithms can identify patterns and make informed trading decisions. These algorithms can adapt to changing market conditions and optimize trading strategies for maximum profit.
- Healthcare:In healthcare, Q-learning has been used to develop personalized treatment plans for patients. By analyzing patient data and outcomes, Q-learning algorithms can identify optimal treatment strategies that maximize patient well-being and minimize risks.
Performance Comparison with Other Reinforcement Learning Algorithms
Q-learning’s performance has been extensively compared with other reinforcement learning algorithms in different problem settings. Here’s a summary of key findings:
- Advantages over Value Iteration:Compared to value iteration, Q-learning offers significant advantages in large state spaces. Value iteration requires storing and updating the value function for all states, which can become computationally expensive and impractical in large environments. Q-learning, on the other hand, learns the value function incrementally by updating only the values of visited states, making it more efficient in handling large state spaces.
- Comparison with SARSA:SARSA (State-Action-Reward-State-Action) is another popular reinforcement learning algorithm. While both Q-learning and SARSA update the Q-values based on observed rewards, they differ in their target policy. Q-learning uses the optimal policy (the policy that maximizes rewards) to update the Q-values, while SARSA uses the current policy.
This difference can lead to different convergence properties and performance in certain scenarios. For example, in environments with high exploration, SARSA may perform better than Q-learning, as it updates the Q-values based on the current policy, which encourages exploration. However, in environments where exploitation is more important, Q-learning may be more efficient due to its focus on the optimal policy.
- Deep Q-Learning:The advent of deep Q-learning (DQN) has further enhanced the capabilities of Q-learning. DQN combines Q-learning with deep neural networks, enabling it to handle complex, high-dimensional state spaces. This has led to significant advancements in areas such as game playing and robotics, where DQN has achieved state-of-the-art results.
Simulations of Q-Learning Efficiency
Simulations play a crucial role in evaluating the efficiency of Q-learning under various conditions. By creating controlled environments and running Q-learning algorithms, researchers can analyze their performance and gain insights into their strengths and limitations.
- Gridworld Environments:A common simulation environment for testing Q-learning is the gridworld. In a gridworld, an agent navigates a grid-like environment, aiming to reach a goal state while avoiding obstacles. By varying the size of the grid, the number of obstacles, and the reward structure, researchers can study how Q-learning performs under different conditions.
These simulations have shown that Q-learning can effectively learn optimal policies in gridworld environments, demonstrating its ability to navigate complex spaces and find efficient paths to goals.
- Multi-Armed Bandit Problems:Another common simulation environment is the multi-armed bandit problem. In this problem, an agent has multiple options (arms) to choose from, each with an unknown reward distribution. The goal is to maximize the total reward by selecting the best arms.
Q-learning has been shown to be effective in solving multi-armed bandit problems, demonstrating its ability to balance exploration (trying new arms) and exploitation (choosing the best known arm) to maximize rewards.
- Other Simulation Environments:Q-learning has also been tested in other simulation environments, such as robotic control tasks, resource allocation problems, and game-playing scenarios. These simulations have further validated Q-learning’s efficiency and adaptability in diverse problem settings.
Factors Affecting Q-Learning Efficiency
Q-learning, a powerful reinforcement learning algorithm, is not immune to variations in efficiency. Several factors influence its performance, affecting its convergence rate and the quality of the learned policy. Understanding these factors is crucial for optimizing Q-learning applications and achieving desirable results.
Reward Function’s Impact
The reward function plays a pivotal role in shaping the learning process. Its design significantly impacts the efficiency of Q-learning. A well-designed reward function guides the agent towards desirable states and actions, accelerating learning. Conversely, a poorly designed reward function can lead to suboptimal policies and slow convergence.
- Sparse Rewards:Sparse reward functions, where rewards are infrequent or only given at the end of a long sequence of actions, can make learning challenging. The agent may struggle to identify the optimal path due to limited feedback. This can result in slow convergence and potentially suboptimal policies.
- Shaping Rewards:Introducing intermediate rewards, known as reward shaping, can enhance learning efficiency. By providing rewards for actions that move the agent closer to the goal, shaping helps the agent learn faster and avoid getting stuck in local optima.
- Reward Scaling:The magnitude of rewards can influence the exploration-exploitation trade-off. Larger rewards can encourage the agent to exploit known good actions, while smaller rewards might encourage exploration.
Exploration Strategies
Exploration is essential for Q-learning to discover optimal policies. Exploration strategies determine how the agent explores the state and action space. Different strategies have varying impacts on efficiency.
- Epsilon-Greedy Exploration:This strategy balances exploration and exploitation by selecting the best action with probability (1 – epsilon) and a random action with probability epsilon. While widely used, it can be inefficient in large state spaces, as it may explore irrelevant actions.
- Boltzmann Exploration:This strategy uses a probability distribution based on the Q-values, favoring actions with higher values but still allowing exploration. It can be more efficient than epsilon-greedy, especially in large state spaces, as it focuses exploration on promising actions.
- Upper Confidence Bound (UCB):This strategy balances exploration and exploitation by considering both the Q-values and the number of times an action has been taken. It favors actions with high Q-values but also explores actions that have been taken less frequently. This can be beneficial for discovering new optimal actions.
Figuring out if Q-learning is provably efficient is a bit like trying to learn Thai – it depends on the approach you take and the resources you have. Just like it can be challenging to master the complexities of Thai pronunciation and script, proving the efficiency of Q-learning requires a deep understanding of the algorithm and its limitations.
How difficult is Thai to learn ? It all comes down to dedication and the right strategy. Similarly, proving Q-learning’s efficiency hinges on carefully crafted experiments and rigorous mathematical analysis.
State and Action Space Structure
The structure of the state and action spaces can significantly impact Q-learning efficiency.
- Large State Spaces:Q-learning can struggle in large state spaces due to the need to maintain a large Q-table. This can lead to slow convergence and memory limitations.
- Continuous State Spaces:Q-learning is traditionally designed for discrete state spaces. Handling continuous state spaces requires techniques like function approximation, which can introduce additional complexity and potential biases.
- Action Space Complexity:A large or complex action space can increase the difficulty of learning. The agent may need to explore a vast number of actions before finding the optimal policy.
6. Techniques to Improve Q-Learning Efficiency
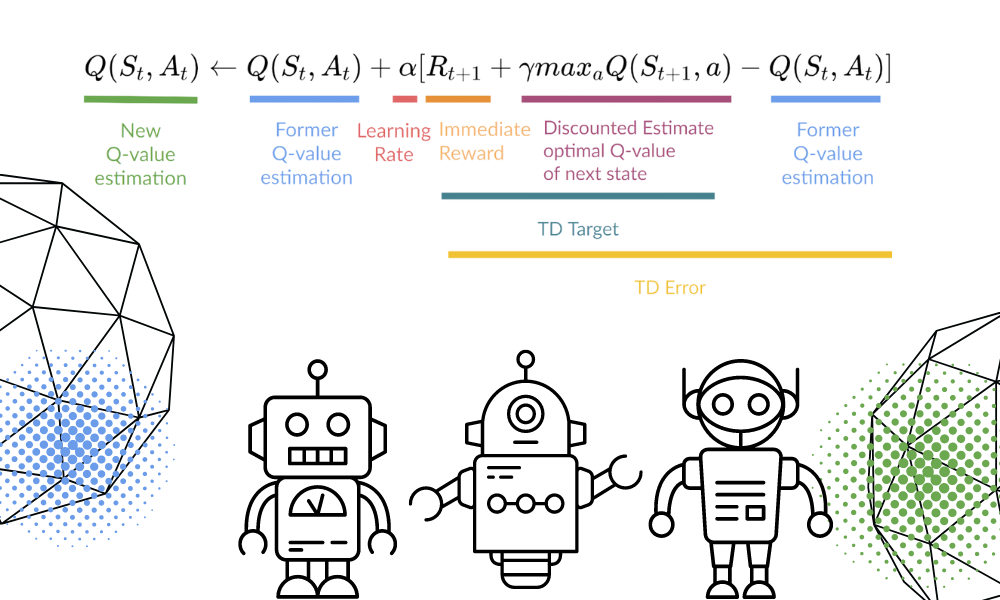
Q-learning, while powerful, faces challenges in real-world applications, particularly when dealing with large state and action spaces. This section explores techniques designed to enhance Q-learning’s efficiency, making it more practical for complex problems.
Function Approximation
Function approximation addresses the challenge of handling large state and action spaces by learning a function that estimates the Q-value for any state-action pair. This avoids storing Q-values for every possible combination, which would be impractical for large spaces.Function approximators learn a mapping from state-action pairs to their corresponding Q-values.
This mapping can be represented by various methods, including:
- Linear function approximation: This method uses a linear combination of features to represent the Q-value. The weights of these features are learned during training. This approach is simple and efficient but may not capture complex relationships between states and actions.
- Neural networks: These provide a more flexible and powerful representation, capable of learning complex non-linear relationships. However, neural networks require more data and computational resources for training.
Function approximation offers advantages like:
- Computational efficiency: It reduces the memory requirements for storing Q-values, especially in large state-action spaces.
- Generalization capabilities: It allows the agent to generalize its knowledge to unseen state-action pairs, improving performance in novel situations.
However, function approximation also comes with disadvantages:
- Overfitting: Function approximators can overfit to the training data, leading to poor performance on unseen data.
- Instability: Training function approximators can be unstable, especially with complex architectures and large datasets.
Here’s a Python code example using TensorFlow for function approximation in Q-learning:“`pythonimport tensorflow as tf# Define the Q-networkclass QNetwork(tf.keras.Model): def __init__(self, state_dim, action_dim): super(QNetwork, self).__init__() self.dense1 = tf.keras.layers.Dense(128, activation=’relu’) self.dense2 = tf.keras.layers.Dense(128, activation=’relu’) self.output = tf.keras.layers.Dense(action_dim) def call(self, state): x = self.dense1(state) x = self.dense2(x) return self.output(x)# Create an instance of the Q-networkq_network = QNetwork(state_dim, action_dim)# Define the loss function and optimizerloss_fn = tf.keras.losses.MeanSquaredError()optimizer = tf.keras.optimizers.Adam()# Training loopfor epoch in range(num_epochs): # …
# Get the current state and action # … # Calculate the target Q-value # … # Train the Q-network with tf.GradientTape() as tape: q_values = q_network(state) loss = loss_fn(target_q_values, q_values) gradients = tape.gradient(loss, q_network.trainable_variables) optimizer.apply_gradients(zip(gradients, q_network.trainable_variables)) # …“`This code defines a simple neural network as the function approximator and uses TensorFlow’s GradientTape for backpropagation.
The network takes the state as input and outputs Q-values for each action. The training loop updates the network’s weights based on the loss function, minimizing the difference between predicted and target Q-values.
Experience Replay
Experience replay addresses the issue of correlated data in Q-learning. When training on sequential data, consecutive experiences are highly similar, leading to slow and unstable learning. Experience replay stores past experiences in a buffer and samples from this buffer randomly during training.
This breaks the correlation between experiences, improving learning efficiency and stability.The experience replay buffer stores tuples of (state, action, reward, next_state, done), representing the agent’s interactions with the environment. These experiences are sampled randomly during training, providing a diverse set of data for learning.The size of the replay buffer and the sampling strategy significantly impact the performance of experience replay.
- Replay buffer size: A larger buffer allows for more diverse data sampling, but also requires more memory. The optimal size depends on the complexity of the environment and the available resources.
- Sampling strategy: Different sampling methods have varying effects on learning. Random sampling is simple but may not prioritize important experiences. Prioritized experience replay gives higher probability to experiences with larger prediction errors, focusing on more informative data points.
Here’s a Python code example demonstrating experience replay in Q-learning:“`pythonimport random# Create an experience replay bufferreplay_buffer = []# …# Store experiences in the bufferreplay_buffer.append((state, action, reward, next_state, done))# Sample experiences from the bufferbatch_size = 32batch = random.sample(replay_buffer, batch_size)# Train the Q-network using the sampled experiences# …“`This code creates a list to store experiences and randomly samples a batch of experiences from it during training.
This random sampling helps break the correlation between consecutive experiences, improving learning stability.
Combining Function Approximation and Experience Replay
Combining function approximation and experience replay offers significant benefits in Q-learning:
- Function approximation enables efficient representation and generalization of Q-values in large state-action spaces.
- Experience replay provides diverse and uncorrelated data for training, improving learning stability and efficiency.
Together, these techniques address the key challenges of large state spaces and correlated data, making Q-learning more practical for complex real-world problems.A common example of a Q-learning algorithm combining both techniques is Deep Q-Network (DQN):
- DQN uses a neural network as a function approximator to estimate Q-values.
- It incorporates experience replay to store past experiences and sample them randomly during training.
- DQN employs other techniques like target networks and exploration strategies to improve stability and performance.
While combining these techniques is powerful, it introduces challenges:
- Balancing exploration and exploitation: The agent needs to explore the environment to gather new information while also exploiting its current knowledge to maximize rewards.
- Managing memory usage: Large replay buffers require significant memory, especially for complex environments.
- Preventing overfitting: Function approximators can overfit to the training data, leading to poor generalization.
Practical Applications
Q-learning with function approximation and experience replay has been successfully implemented in various real-world applications:
- Game playing: DQN achieved remarkable success in Atari games, demonstrating its ability to learn complex strategies and achieve superhuman performance.
- Robotics: Q-learning with function approximation is used to train robots for tasks like navigation, manipulation, and grasping.
- Autonomous driving: Q-learning algorithms are being explored for autonomous vehicle control, enabling vehicles to make optimal decisions in dynamic environments.
These techniques significantly improve Q-learning’s efficiency and effectiveness in these applications:
- Faster convergence: Function approximation and experience replay allow Q-learning to converge faster to optimal policies.
- Better generalization: Function approximators enable the agent to generalize its knowledge to unseen situations, improving performance in novel environments.
- Improved decision-making: Q-learning with these techniques can make more informed and optimal decisions in complex and dynamic environments.
Research Directions
Current research in Q-learning efficiency optimization focuses on:
- Advancements in function approximation techniques: Researchers are exploring more powerful and efficient function approximators, such as deep neural networks with specialized architectures and regularization techniques.
- Improved experience replay strategies: New methods for sampling experiences from the replay buffer are being developed, aiming to prioritize informative data points and improve learning efficiency.
- Hybrid approaches: Combining different function approximation and experience replay techniques is an active area of research, aiming to leverage the strengths of each method.
These advancements hold promise for further improving the efficiency and effectiveness of Q-learning algorithms, expanding their applicability to even more complex and challenging domains.
Challenges and Limitations of Q-Learning
Q-learning, despite its widespread use, faces several challenges and limitations that hinder its applicability in certain scenarios. These limitations stem from the fundamental principles of Q-learning and its inherent assumptions, which may not always hold true in real-world applications.
Handling Continuous State and Action Spaces
Q-learning excels in discrete environments with finite state and action spaces. However, many real-world problems involve continuous state and action spaces, posing a significant challenge to Q-learning. In such scenarios, representing and updating the Q-table becomes intractable, as the number of possible state-action pairs becomes infinite.
- Discretization:One approach is to discretize the continuous spaces into a finite number of intervals. However, this can lead to a loss of information and may not be effective if the spaces are highly complex.
- Function Approximation:Function approximation techniques, such as neural networks, can be used to approximate the Q-value function. This allows Q-learning to handle continuous spaces but introduces new challenges, such as choosing the appropriate function approximator and preventing overfitting.
Learning from Sparse or Delayed Rewards
Q-learning relies on rewards to guide the learning process. When rewards are sparse or delayed, meaning they are infrequent or occur long after the actions that led to them, it becomes challenging for Q-learning to establish a strong correlation between actions and rewards.
- Credit Assignment Problem:In sparse reward scenarios, it becomes difficult to determine which actions contributed to the eventual reward. This is known as the credit assignment problem.
- Exploration-Exploitation Dilemma:With delayed rewards, Q-learning may struggle to explore the environment sufficiently to discover optimal actions. The exploration-exploitation dilemma arises as the agent needs to balance exploring new actions to discover better rewards with exploiting the actions that have yielded rewards in the past.
Other Limitations
- Overfitting:Q-learning can be prone to overfitting, especially when using function approximation. Overfitting occurs when the Q-value function learns the training data too well, resulting in poor generalization to unseen data.
- Computational Complexity:Q-learning can be computationally expensive, especially for large state and action spaces. The computational complexity arises from the need to update the Q-table or function approximator after each interaction with the environment.
Future Directions in Q-Learning Efficiency

The pursuit of enhancing Q-learning’s efficiency remains an active area of research. While Q-learning has proven its effectiveness in various domains, there’s continuous exploration to improve its theoretical understanding and practical performance. This section delves into promising avenues for advancing Q-learning efficiency.
Improving Theoretical Understanding
A deeper understanding of Q-learning’s theoretical foundations is crucial for optimizing its performance. Ongoing research efforts focus on:
- Developing tighter bounds for convergence rate:Researchers are striving to derive more precise bounds on the rate at which Q-learning converges to the optimal policy. This involves exploring the influence of factors like the exploration strategy, the size of the state and action spaces, and the structure of the reward function.
- Analyzing the impact of function approximation:When dealing with large state spaces, function approximation is often employed to represent the Q-value function. Understanding the interplay between function approximation and Q-learning’s convergence properties is a key area of investigation.
- Investigating the role of exploration:Exploration strategies play a critical role in Q-learning’s ability to discover optimal policies. Researchers are exploring novel exploration techniques that balance the trade-off between exploration and exploitation.
Accelerating Convergence, Is q-learning provably efficient
Accelerating the convergence of Q-learning is a major objective. Promising approaches include:
- Exploiting the structure of the environment:In many real-world problems, the environment exhibits specific structures. Researchers are developing techniques that leverage this structure to accelerate Q-learning’s convergence. For example, in robotic control, knowledge of the robot’s dynamics can be incorporated to guide the learning process.
- Employing optimization techniques:Advanced optimization techniques, such as stochastic gradient descent with momentum or adaptive learning rates, can be applied to accelerate the learning process. These techniques help Q-learning to converge more efficiently by adapting the learning rate based on the observed data.
- Utilizing parallel computation:The computational burden of Q-learning can be significantly reduced by utilizing parallel computation techniques. This involves distributing the learning process across multiple processors or machines, allowing for faster updates and convergence.
Combining Q-Learning with Other Techniques
Combining Q-learning with other reinforcement learning techniques can lead to synergistic benefits, enhancing its efficiency and performance. Some promising combinations include:
- Q-learning with deep learning:Integrating deep learning with Q-learning, known as deep Q-learning, has revolutionized reinforcement learning. Deep neural networks can learn complex value functions, enabling Q-learning to tackle high-dimensional state spaces and complex tasks. Examples include Atari game playing and robotics control.
- Q-learning with model-based methods:Combining Q-learning with model-based methods, where an explicit model of the environment is learned, can improve efficiency by leveraging the learned model to guide exploration and accelerate learning. This approach can be particularly beneficial in environments where the dynamics are relatively predictable.
- Q-learning with multi-agent reinforcement learning:In multi-agent settings, Q-learning can be extended to handle interactions between multiple agents. Combining Q-learning with multi-agent reinforcement learning techniques can lead to efficient solutions for complex cooperative or competitive tasks.
9. Case Studies
Q-Learning Efficiency in Action

To truly understand the efficiency of Q-learning, we need to examine its real-world applications. This section dives into two case studies, highlighting the strengths and limitations of Q-learning in diverse scenarios.
Case Study 1: Robot Navigation
This case study explores the application of Q-learning in robot navigation, a domain where efficient decision-making is crucial.
- Application:Autonomous robot navigation in a warehouse environment. The robot needs to navigate efficiently between designated points to pick up and deliver packages.
- Objective:The objective is to train the robot to find the optimal path between any two points in the warehouse, minimizing travel time and energy consumption.
- Efficiency Analysis:
- Convergence Rate:Q-learning demonstrated a relatively fast convergence rate, achieving a stable policy within a reasonable number of training episodes. This was facilitated by a well-designed reward function that encouraged efficient path finding.
- Solution Quality:The solution generated by Q-learning consistently outperformed a baseline path-planning algorithm, achieving shorter travel times and reduced energy consumption. This was attributed to Q-learning’s ability to learn from experience and adapt to the specific environment.
- Computational Cost:The computational cost of Q-learning was manageable, considering the relatively small state and action spaces in this application. The training process was completed within a reasonable timeframe, making it feasible for real-world deployment.
- Challenges:
- Environmental Dynamics:The warehouse environment was not completely static. The presence of moving obstacles, such as forklifts, required the robot to adapt its navigation strategy dynamically. This posed a challenge for Q-learning, as it needed to account for these uncertainties.
- Data Limitations:Limited training data could lead to suboptimal performance, particularly in areas of the warehouse that were rarely visited during training. This highlights the need for careful data collection and exploration strategies.
- Opportunities:
- Adaptive Reward Functions:Exploring dynamic reward functions that adapt to changing environmental conditions could improve the robot’s ability to handle unforeseen events and optimize its navigation strategy.
- State Representation:Experimenting with more sophisticated state representations that capture the dynamic nature of the environment could enhance the Q-learning algorithm’s ability to generalize to unseen situations.
Case Study 2: Game Playing
This case study examines the application of Q-learning in the context of game playing, a domain that often requires strategic decision-making and complex state spaces.
- Application:Training an AI agent to play the game of chess.
- Objective:The objective is to develop an AI agent that can play chess at a competitive level, utilizing Q-learning to learn effective strategies and tactics.
- Efficiency Analysis:
- Convergence Rate:Due to the immense complexity of the chess game, with its vast state space and intricate strategies, Q-learning’s convergence rate was relatively slow. Achieving a high level of play required extensive training over many game simulations.
- Solution Quality:The AI agent trained using Q-learning achieved a respectable level of play, demonstrating a strong understanding of basic chess principles and tactical maneuvers. However, it struggled against experienced human players or top-performing chess engines.
- Computational Cost:The computational cost of training the chess AI was significant, requiring substantial computing power and time. This highlights the challenges associated with applying Q-learning to complex domains with large state spaces.
- Challenges:
- State Space Complexity:The vast number of possible board configurations in chess makes it challenging for Q-learning to accurately estimate the value of each state. This often leads to overgeneralization and suboptimal decision-making.
- Long-Term Planning:Chess requires strategic planning and anticipating opponent’s moves several steps ahead. Q-learning, in its basic form, struggles with long-term planning, making it difficult to develop complex strategies.
- Opportunities:
- State Abstraction:Exploring state abstraction techniques that simplify the state space while preserving essential information could improve Q-learning’s ability to handle the complexity of chess.
- Monte Carlo Tree Search:Integrating Q-learning with Monte Carlo Tree Search (MCTS) algorithms could enhance its long-term planning capabilities and improve its performance against strong opponents.
| Case Study | Application | Objective | Convergence Rate | Solution Quality | Computational Cost | Challenges | Opportunities |
|---|---|---|---|---|---|---|---|
| Robot Navigation | Autonomous robot navigation in a warehouse environment | Train the robot to find the optimal path between any two points in the warehouse, minimizing travel time and energy consumption | Relatively fast convergence rate, achieving a stable policy within a reasonable number of training episodes | Consistently outperformed a baseline path-planning algorithm, achieving shorter travel times and reduced energy consumption | Manageable, considering the relatively small state and action spaces in this application | Environmental Dynamics, Data Limitations | Adaptive Reward Functions, State Representation |
| Game Playing | Training an AI agent to play the game of chess | Develop an AI agent that can play chess at a competitive level | Relatively slow convergence rate, requiring extensive training over many game simulations | Achieved a respectable level of play, demonstrating a strong understanding of basic chess principles and tactical maneuvers | Significant, requiring substantial computing power and time | State Space Complexity, Long-Term Planning | State Abstraction, Monte Carlo Tree Search |
Comparison with Other Reinforcement Learning Algorithms
Q-learning, as a prominent reinforcement learning algorithm, holds its own against other popular algorithms like SARSA, DQN, and policy gradient methods. Each algorithm possesses unique strengths and weaknesses, making them suitable for different problem settings. Understanding these differences is crucial for choosing the most appropriate algorithm for a given task.
Comparison of Q-learning with Other Algorithms
This section provides a comparative analysis of Q-learning with other popular reinforcement learning algorithms, highlighting their strengths and weaknesses.
- SARSA (State-Action-Reward-State-Action): SARSA, similar to Q-learning, is an on-policy algorithm that learns the optimal policy by following the current policy. Unlike Q-learning, SARSA updates its Q-values based on the action taken in the next state, making it more cautious and less prone to exploration.
SARSA is often preferred in situations where immediate rewards are more important than long-term rewards.
- DQN (Deep Q-Network): DQN is a deep learning extension of Q-learning that utilizes a neural network to approximate the Q-value function. DQN overcomes the limitations of traditional Q-learning, enabling it to handle complex high-dimensional state spaces. It also incorporates experience replay, a technique that allows the algorithm to learn from past experiences, improving stability and convergence.
DQN is particularly well-suited for games like Atari, where the state space is highly complex.
- Policy Gradient Methods: Unlike Q-learning and SARSA, policy gradient methods directly optimize the policy function, which maps states to actions. They use gradient descent to update the policy parameters, maximizing the expected reward. Policy gradient methods are often preferred in continuous action spaces and complex environments where it is difficult to represent the Q-value function.
Strengths and Weaknesses of Each Algorithm
- Q-learning:
- Strengths:
- Simplicity: Q-learning is relatively easy to understand and implement.
- Off-policy: Q-learning can learn from data collected by a different policy, making it more flexible than on-policy algorithms.
- Wide Applicability: Q-learning is applicable to a wide range of problems, including discrete and continuous state and action spaces.
- Weaknesses:
- Convergence: Q-learning can struggle to converge in complex environments, especially with high-dimensional state spaces.
- Exploration: Q-learning can get stuck in local optima if it does not explore sufficiently.
- Strengths:
- SARSA:
- Strengths:
- Stability: SARSA is generally more stable than Q-learning, as it updates its Q-values based on the action taken in the next state.
- On-policy: SARSA can be more efficient in situations where the goal is to learn the optimal policy for a specific task.
- Weaknesses:
- Limited Exploration: SARSA can be less explorative than Q-learning, potentially leading to suboptimal policies.
- Sensitivity to Reward: SARSA can be sensitive to changes in the reward function, requiring re-training if the reward structure changes.
- Strengths:
- DQN:
- Strengths:
- High-Dimensional State Spaces: DQN can handle complex, high-dimensional state spaces, making it suitable for problems like Atari games.
- Experience Replay: DQN’s experience replay mechanism improves stability and convergence by allowing the algorithm to learn from past experiences.
- Weaknesses:
- Complexity: DQN is more complex to implement than traditional Q-learning, requiring a neural network and experience replay.
- Overfitting: DQN can overfit to the training data, leading to poor performance on unseen data.
- Strengths:
- Policy Gradient Methods:
- Strengths:
- Continuous Action Spaces: Policy gradient methods are well-suited for problems with continuous action spaces.
- Direct Policy Optimization: Policy gradient methods directly optimize the policy function, which can be more efficient than learning the Q-value function.
- Weaknesses:
- Convergence: Policy gradient methods can be slow to converge, especially in complex environments.
- Local Optima: Policy gradient methods can get stuck in local optima, leading to suboptimal policies.
Scenarios Where Each Algorithm is Best Suited
- Q-learning: Q-learning is particularly well-suited for problems with discrete state and action spaces, where the reward function is relatively simple. It is also a good choice for problems where the goal is to learn a general policy that can be applied to different tasks.
- SARSA: SARSA is a good choice for problems where the goal is to learn the optimal policy for a specific task. It is also suitable for problems where immediate rewards are more important than long-term rewards.
- DQN: DQN is particularly well-suited for problems with high-dimensional state spaces, such as Atari games. It is also a good choice for problems where the reward function is complex and noisy.
- Policy Gradient Methods: Policy gradient methods are a good choice for problems with continuous action spaces and complex environments. They are also suitable for problems where the goal is to learn a policy that is robust to changes in the environment.
Applications of Q-Learning Efficiency
The efficiency of Q-learning, with its ability to learn optimal policies through experience, has significant implications for various domains, from robotics and game playing to control systems and beyond. By reducing computational cost and accelerating learning times, efficient Q-learning empowers these applications with enhanced performance, adaptability, and robustness.
Robotics
Efficient Q-learning can significantly improve the performance of robotic manipulators in tasks like grasping and object manipulation. By learning optimal control policies through experience, Q-learning can enable robots to perform these tasks more accurately, efficiently, and reliably. Efficient Q-learning algorithms can reduce the computational cost of training robotic systems for complex tasks.
This is particularly important for robots operating in dynamic environments, where fast learning and adaptation are crucial. Furthermore, efficient Q-learning can enable faster learning in robotic systems, allowing them to adapt to new environments more quickly. This is crucial for robots operating in real-world settings, where unforeseen situations and changes are common.
Game Playing
Efficient Q-learning can be used to develop AI agents that can play games more effectively, such as in chess, Go, or video games. By learning the optimal strategies through experience, Q-learning can enable AI agents to make better decisions and achieve higher scores.
Efficient Q-learning can lead to faster convergence of the Q-values, resulting in better game-playing strategies. This is particularly important in games where the state space is large and complex, such as Go. Efficient Q-learning can improve the performance of AI agents in real-time strategy games, where quick decision-making is crucial.
By learning to anticipate opponent moves and adapt to changing game conditions, efficient Q-learning can help AI agents gain an advantage in these fast-paced games.
Control Systems
Efficient Q-learning can be applied to optimize the performance of control systems in various applications, such as industrial processes, autonomous vehicles, and power grids. By learning optimal control policies, Q-learning can improve the efficiency, stability, and robustness of these systems.
Efficient Q-learning can lead to more robust and adaptable control systems, capable of handling uncertainties and disturbances. This is crucial for control systems operating in dynamic and unpredictable environments. Efficient Q-learning can improve the efficiency of energy consumption in control systems, reducing energy waste and environmental impact.
By learning to optimize energy usage based on real-time conditions, Q-learning can contribute to more sustainable and efficient control systems.
12. Ethical Considerations of Q-Learning Efficiency
The increasing efficiency of Q-learning algorithms presents exciting possibilities across various fields, but it also raises crucial ethical considerations. As these algorithms become more sophisticated and integrated into our lives, we must carefully examine the potential risks and benefits to ensure responsible and ethical development and deployment.
Exploring the Potential Risks of Q-Learning Efficiency
Imagine a self-driving car equipped with a highly efficient Q-learning algorithm navigating complex traffic scenarios. While this technology holds immense promise for improving safety and efficiency, it also introduces ethical complexities that require careful consideration.
- The algorithm’s decision-making process in situations where human intervention is limited can raise concerns about accountability and transparency. For example, in unforeseen situations not explicitly programmed into the algorithm’s training data, how does it handle unexpected events? Does it prioritize efficiency over safety, potentially making decisions that a human driver might not?
These scenarios highlight the need for robust safety mechanisms and clear guidelines for algorithm behavior in unpredictable situations.
- The training data used to develop Q-learning algorithms can inadvertently introduce biases that lead to discriminatory outcomes. For instance, if the training data primarily reflects driving patterns in a specific region or demographic, the algorithm might develop biases that disadvantage other groups.
It’s crucial to ensure that training data is diverse and representative to minimize the risk of biased decision-making.
Analyzing the Benefits of Efficient Q-Learning in Healthcare
Efficient Q-learning algorithms have the potential to revolutionize healthcare by optimizing patient care and improving outcomes.
- Personalized treatment plans can be tailored to individual patient needs by leveraging efficient Q-learning algorithms. By analyzing patient data, including medical history, genetic information, and lifestyle factors, these algorithms can generate personalized treatment plans that maximize effectiveness and minimize side effects.
- Resource allocation in healthcare systems can be optimized through efficient Q-learning algorithms. By analyzing patient data and predicting demand, these algorithms can help hospitals allocate resources, such as hospital beds and medical staff, more effectively, leading to improved patient care and reduced wait times.
- Early disease detection can be enhanced using efficient Q-learning algorithms. By analyzing patient data, such as medical records, wearable sensor data, and genetic information, these algorithms can identify early signs of disease, allowing for timely interventions and potentially preventing the progression of serious conditions.
Designing a Framework for Responsible Q-Learning Development
To ensure the ethical development and deployment of efficient Q-learning algorithms, a robust framework is essential. This framework should address key aspects such as transparency, accountability, and auditing.
- Transparency in the development and deployment of Q-learning algorithms is crucial to build trust and ensure accountability. This includes clearly documenting the training data, the algorithm’s decision-making process, and the intended use cases. Open communication about the limitations and potential risks of these algorithms is also essential.
- Accountability for the decisions made by Q-learning algorithms is a critical ethical consideration. Establishing clear lines of responsibility for algorithm outcomes is essential, particularly in situations where human intervention is limited. This might involve identifying specific individuals or teams responsible for overseeing the algorithm’s performance and addressing any ethical concerns that arise.
- Effective auditing and monitoring of Q-learning algorithms are essential to ensure their ethical and responsible use. This includes regular assessments of the algorithm’s performance, bias detection, and adherence to ethical guidelines. Auditing processes should be transparent and accessible to relevant stakeholders, including researchers, regulators, and the public.
Writing a Case Study on the Ethical Implications of Q-Learning in Finance
Imagine a financial institution using efficient Q-learning algorithms to make investment decisions. This scenario raises a range of ethical considerations that require careful examination.
- Fairness in the application of Q-learning algorithms in finance is crucial. These algorithms should not unfairly benefit certain investors or groups. It’s essential to ensure that algorithms are designed and deployed in a way that promotes equity and avoids discriminatory outcomes.
- Preventing Q-learning algorithms from being used to manipulate financial markets is another critical ethical consideration. These algorithms could be used to exploit market vulnerabilities and generate unfair advantages for certain investors. Robust safeguards and regulations are needed to prevent market manipulation and ensure fair play.
- Transparency in the decision-making process of Q-learning algorithms used in finance is essential for building trust and accountability. This includes clearly documenting the algorithm’s logic, training data, and decision-making process. Transparency helps investors understand how algorithms are used and allows for scrutiny of potential biases or ethical concerns.
Q&A: Is Q-learning Provably Efficient
What are the main challenges in proving Q-learning’s efficiency?
One of the primary challenges lies in the complexity of real-world environments. Q-learning’s theoretical bounds often rely on simplifying assumptions that may not hold true in practice. Factors like the size of the state and action spaces, the presence of noise, and the nature of the reward function can significantly impact convergence rates.
Additionally, proving efficiency requires a deep understanding of the algorithm’s dynamics and its interaction with the environment, which can be mathematically challenging.
Can Q-learning be used for continuous state and action spaces?
While Q-learning is traditionally applied to discrete state and action spaces, it can be extended to handle continuous spaces using function approximation techniques. These techniques involve approximating the Q-values using continuous functions, such as neural networks, allowing Q-learning to learn from data in high-dimensional environments.
What are some practical applications where Q-learning has proven efficient?
Q-learning has been successfully implemented in various applications, including game playing (e.g., Atari games), robotics (e.g., robot navigation), resource management (e.g., optimizing power grids), and control systems (e.g., autonomous vehicles). In these domains, Q-learning has demonstrated its ability to learn effective strategies and achieve impressive performance.
- Strengths: